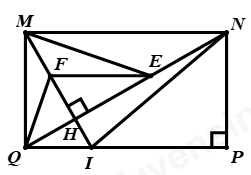
Cho hình chữ nhật \(MNPQ(MN > NP),MH\) vuông góc với \(QN\) tại \(H\). a) Chứng minh:\(\Delta MNH \sim

Câu hỏi số 543968:

Vận dụng

Cho hình chữ nhật \(MNPQ(MN > NP),MH\) vuông góc với \(QN\) tại \(H\).

a) Chứng minh:\(\Delta MNH \sim \Delta NQP\)

b) Chứng minh \(M{N^2} = QN.NH\)

c) Lấy \(E,F\) lần lượt là trung điểm của \(NH,MH\). Chứng minh: \(\Delta MNE \sim \Delta QMF\).

d) \(MH\) cắt \(PQ\) tại \(I\). Tính diện tích \(\Delta MNI\), biết \(QI = \dfrac{1}{2}QP\) và diện tích \(\Delta QHI\) là \(3c{m^2}\).

Quảng cáo

Xem lời giải

Câu hỏi:543968

Phương pháp giải

a) \(\Delta MNH \sim \Delta NQP(g.g)\)

b) \(\dfrac{{QN}}{{QP}} = \dfrac{{QN}}{{MN}} \Rightarrow M{N^2} = QN.NH\)

c) \(\Delta MNH \sim \Delta NQP(cmt) \Rightarrow \angle HMQ = \angle MNQ\)

\(\Delta MNH \sim \Delta NQP(cmt) \Rightarrow \dfrac{{MF}}{{NE}} = \dfrac{{MQ}}{{MN}}\)

\( \Rightarrow \Delta MNE \sim \Delta QME(c.g.c)\)

d) Diện tích tam giác vuông bằng một phần hai tích hai cạnh góc vuông.

Chứng minh: \(HN = 2QH\) và \(MI = 3HI \Rightarrow {S_{\Delta MNI}} = 6.{S_{\Delta QHI}}\)

Giải chi tiết

Mặt khác, \(\angle NPQ = {90^0}\)

Vì \(MH \bot QN\) tại \(H\left( {gt} \right) \Rightarrow \angle MHN = {90^0}\)

Do đó, \(\angle MHN = \angle NPQ = {90^0}\)

Xét \(\Delta MNH\) và \(\Delta NQP\) có:

\(\left. \begin{array}{l}\angle MHN = \angle NPQ = {90^0}\left( {cmt} \right)\\\angle MNH = \angle NQP\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta MNH \sim \Delta NQP\left( {g.g} \right)\)

b) Vì \(\Delta MNH \sim \Delta NQP\left( {cmt} \right) \Rightarrow \dfrac{{MN}}{{NH}} = \dfrac{{QN}}{{QP}}\) (đpcm)

\(MNPQ\) là hình chữ nhật \( \Rightarrow MN = QP\) (tính chất hình chữ nhật)

Do đó, \(\dfrac{{MN}}{{NH}} = \dfrac{{QN}}{{MN}} \Rightarrow M{N^2} = QN.NH\) (đpcm)

c) Vì \(\Delta MNH \sim \Delta NQP(cmt) \Rightarrow \angle HMN = \angle PNQ\) (hai góc tương ứng)

Ta có: \(\angle HMN + \angle HMQ = 90^\circ \Leftrightarrow \angle PNQ + \angle HMQ = 90^\circ \)

Mà: \(\angle PNQ + \angle MNQ = 90^\circ \)

Ta có: \(\angle QMH + \angle HMN = {90^0}\) (do \(MNPQ\) là hình chữ nhật)

\(\angle HMN + \angle MNH = {90^0}\) (do \(MH \bot QN\))

\( \Rightarrow \angle QMH = \angle MNH\) (cùng phụ với \(\angle HMN\))

\( \Rightarrow \angle QMH = \angle MNQ\)

Vì \(\Delta MNH \sim \Delta NQP(cmt) \Rightarrow \dfrac{{MH}}{{NH}} = \dfrac{{NP}}{{QP}}\)

Ta có: \(\dfrac{{MH}}{{NH}} = \dfrac{{MF}}{{NE}};\quad \dfrac{{NP}}{{QP}} = \dfrac{{MQ}}{{MN}}\quad \Rightarrow \dfrac{{MF}}{{NE}} = \dfrac{{MQ}}{{MN}}\)

Xét \(\Delta MNH\) và \(\Delta NQP\) có:

\(\left. \begin{array}{l}\angle HMQ = \angle MNQ(cmt)\\\dfrac{{MF}}{{NE}} = \dfrac{{MQ}}{{MN}}(cmt)\end{array} \right\} \Rightarrow \Delta MNH \sim \Delta NQP(c.g.c)\)

d) Ta có: \(QI = \dfrac{1}{2}QP\)\( \Rightarrow \dfrac{{QI}}{{QP}} = \dfrac{1}{2}\) mà \(QP = MN\) (do \(MNPQ\) là hình chữ nhật) \( \Rightarrow \dfrac{{QI}}{{MN}} = \dfrac{1}{2}\)

\(MNPQ\) là hình chữ nhật \( \Rightarrow MN//PQ\) mà \(I \in PQ \Rightarrow MN//IQ\)

\(MN//IQ(cmt) \Rightarrow \Delta QHI \sim \Delta NHM(g.g) \Rightarrow \dfrac{{QI}}{{MN}} = \dfrac{{QH}}{{HN}} = \dfrac{{HI}}{{MH}} = \dfrac{1}{2}\)

Vì \(\dfrac{{QH}}{{HN}} = \dfrac{1}{2} \Rightarrow \left\{ \begin{array}{l}HN = 2QH\\MH = 2HI\end{array} \right.\). Ta có : \(MI = MH + HI \Rightarrow MI = 3HI\)

\({S_{\Delta MNI}} = \dfrac{1}{2}MI.NH = \dfrac{1}{2}.3HI.2QH = 6.\dfrac{1}{2}.HI.QH = 6.{S_{\Delta QHI}} = 6.3 = 18(c{m^2})\)

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link