Cho cơ hệ gồm một lò xo có khối lượng không đáng kể có độ cứng \(k = 120N/m\), một đầu
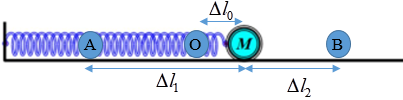
Cho cơ hệ gồm một lò xo có khối lượng không đáng kể có độ cứng \(k = 120N/m\), một đầu gắn với điểm cố định, một đầu gắn với vật có khối lượng \(m = 100g\), vật có thể trượt trên mặt phẳng ngang có hệ số ma sát \(\mu = 0,6\). Ban đầu đưa vật đến vị trí lò xo nén 12cm rồi thả ra không vận tốc ban đầu. Xác định độ dãn cực đại của lò xo và tốc độ cực đại của vật sau đó.
Quảng cáo
Biến thiên cơ năng bằng công của lực ma sát: \(\Delta {\rm{W}} = {A_{m{\rm{s}}}}\)
Công thức tính công: \(A = F.s.cos\alpha \)
Cơ năng của vật chịu tác dụng của lực đàn hồi: \(W = \dfrac{1}{2}k.\Delta {l^2} + \dfrac{1}{2}m{v^2}\)
Cơ năng tại A: \({W_A} = \dfrac{1}{2}k.\Delta l_1^2\)
Cơ năng tại B: \({W_B} = \dfrac{1}{2}k.\Delta l_2^2\)
Độ biến thiên cơ năng bằng công của lực ma sát nên:
\({W_A} - {W_B} = {A_{Fms}}\)
\( \Leftrightarrow \dfrac{1}{2}k.\Delta l_1^2 - \dfrac{1}{2}k.\Delta l_2^2 = {F_{ms}}.BA.cos180\)
\( \Leftrightarrow \dfrac{1}{2}k{\left( {\Delta {l_2}} \right)^2} - \dfrac{1}{2}k{\left( {\Delta {l_1}} \right)^2} = - {F_{m{\rm{s}}}}.\left( {\Delta {l_1} + \Delta {l_2}} \right)\)
\( \Leftrightarrow \dfrac{1}{2}k.\left( {\Delta {l_2} + \Delta {l_1}} \right).\left( {\Delta {l_2} - \Delta {l_1}} \right) = - {F_{m{\rm{s}}}}.\left( {\Delta {l_1} + \Delta {l_2}} \right)\)
\( \Leftrightarrow \dfrac{1}{2}k\left( {\Delta {l_2} - \Delta {l_1}} \right) = - \mu mg\)
\( \Leftrightarrow \dfrac{1}{2}k\left( {\Delta {l_2} - 0,12} \right) = - 0,6.0,1.10\)
\( \Leftrightarrow \Delta {l_2} = 0,11m = 11cm\)
Vận tốc cực đại tại vị trí \({F_{m{\rm{s}}}} = {F_{dh}}\)
\( \Rightarrow \Delta {l_0} = \dfrac{{{F_{m{\rm{s}}}}}}{k} = \dfrac{{\mu mg}}{k} = \dfrac{{0,6.0,1.10}}{{120}} = 0,005m\)
Cơ năng tại O: \({W_O} = \dfrac{1}{2}k.\Delta l_0^2 + \dfrac{1}{2}mv_0^2\)
Độ biến thiên cơ năng bằng công của lực ma sát nên:
\({W_A} - {W_O} = {A_{Fms}}\)
\( \Leftrightarrow \dfrac{1}{2}k.\Delta l_1^2 - \left( {\dfrac{1}{2}k.\Delta l_0^2 + \dfrac{1}{2}mv_0^2} \right) = {F_{ms}}.AO.cos180\)
\( \Leftrightarrow \dfrac{1}{2}k.\Delta l_1^2 - \left( {\dfrac{1}{2}k.\Delta l_0^2 + \dfrac{1}{2}mv_0^2} \right) = - \mu mg.\left( {\Delta {l_1} - \Delta {l_0}} \right)\)
\( \Leftrightarrow \dfrac{1}{2}k.\Delta l_1^2 - \left( {\dfrac{1}{2}k.\Delta l_0^2 + \dfrac{1}{2}mv_0^2} \right) = - \mu mg.\left( {\Delta {l_1} - \Delta {l_0}} \right)\)
\( \Leftrightarrow k.\Delta l_1^2 - k.\Delta l_0^2 - mv_0^2 = - 2\mu mg.\left( {\Delta {l_1} - \Delta {l_0}} \right)\)
\( \Leftrightarrow mv_0^2 = k.\Delta l_1^2 - k.\Delta l_0^2 + 2\mu mg.\left( {\Delta {l_1} - \Delta {l_0}} \right)\)
\( \Leftrightarrow {v_0} = \sqrt {\dfrac{{k.\left( {\Delta l_1^2 - \Delta l_0^2} \right) + 2\mu mg.\left( {\Delta {l_1} - \Delta {l_0}} \right)}}{m}} \)
\( \Rightarrow {v_0} = \sqrt {\dfrac{{120.\left( {0,{{12}^2} - 0,{{005}^2}} \right) + 2.0,6.0,1.10.\left( {0,12 - 0,005} \right)}}{{0,1}}} \)
\( \Rightarrow {v_0} = 4,32m/s\)
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> 2K11 học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, Kiến thức cập nhật theo chương trình mới nhất. Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
