Một lò xo nhẹ có độ cứng k = 100N/m, đầu trên gắn cố định, đầu dưới treo quả cầu nhỏ

Câu hỏi số 554135:

Vận dụng cao

Một lò xo nhẹ có độ cứng k = 100N/m, đầu trên gắn cố định, đầu dưới treo quả cầu nhỏ M có khối lượng 500g sao cho vật có thể dao động không ma sát theo phương thẳng đứng. Ban đầu vật tựa vào giá đỡ nằm ngang để lò xo bị nén 7,5cm. Cho giá đỡ chuyển động thẳng đứng xuống dưới với gia tốc \(a = 10m/{s^2}\). Lấy \(g = 10m/{s^2}\), sau khi M rời khỏi giá nó dao động điều hòa. Kể từ khi giá đỡ chuyển động cho đến khi lực đàn hồi của lò xo đạt giá trị lớn nhất lần đầu tiên, quãng đường mà vật M đi được là

A. 15cm.

B. 17,5cm.

C. 20cm.

D. 22,5cm.

Đáp án đúng là: D

Quảng cáo

Xem lời giải

Câu hỏi:554135

Phương pháp giải

+ Độ dãn của lò xo tại vị trí cân bằng: \(\Delta l = \dfrac{{mg}}{k}\)

+ Tần số góc: \(\omega = \sqrt {\dfrac{k}{m}} \)

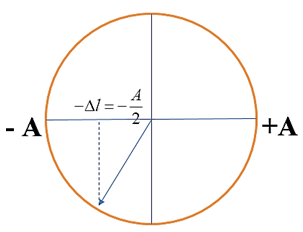
+ Sử dụng VTLG

+ Sử dụng công thức liên hệ s,v,a của chuyển động thẳng biến đổi đều: \({v^2} - v_0^2 = 2a{\rm{s}}\)

Giải chi tiết

Chọn chiều dương hướng xuống, gốc O trùng VTCB. Ta có:

Độ dãn của lò xo tại VTCB:

\(\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,5.10}}{{100}} = 0,05m = 5cm\)

Tần số góc của dao động:

\(\omega = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{{100}}{{0,5}}} = 10\sqrt 2 ra{\rm{d}}/s \Rightarrow T = \dfrac{{\pi \sqrt 2 }}{{10}}s\)

Ban đầu \({F_{dh}} = N\) với N là phản lực của giá đỡ tác dụng lên vật.

Vật bắt đầu rời khỏi giá đỡ khi \(N = 0\) khi đó \({F_{dh}} = 0\) \( \Rightarrow x = - \Delta l = - 5cm\)

Như vậy, hệ đến vị trí lò xo không biến dạng thì vật sẽ tách ra khỏi giá và dao động điều hòa

Quãng đường mà giá rơi được đến thời điểm đó là: \(s = 7,5cm = 0,075m\)

Vận tốc của vật tại vị trí bắt đầu tách ra đó:

\({v^2} - v_0^2 = 2g{\rm{s}} \Leftrightarrow {v^2} - {0^2} = 2.10.0,075\)

\( \Rightarrow v = \dfrac{{\sqrt 6 }}{2}m/s = 50\sqrt 6 cm/s\)

Áp dụng công thức độc lập tại vị trí này cho vật, ta có:

\({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} \Rightarrow A = \sqrt {{{\left( { - 5} \right)}^2} + {{\left( {\dfrac{{50\sqrt 6 }}{{10\sqrt 2 }}} \right)}^2}} = 10cm\)

Lực đàn hồi của lò xo đạt giá trị lớn nhất ở vị trí biên dương

Quãng đường mà vật M đi được kể từ khi thả cho giá đỡ rơi tự do đến khi lực đàn hồi của lò xo đạt giá trị lớn nhất lần đầu tiên là:

\(S = s + \dfrac{A}{2} + A = 7,5 + 5 + 10 = 22,5cm\)

Đáp án cần chọn là: D

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.