Trong các trò chơi thể thao mạo hiểm, việc ứng dụng khoa học nhằm kiểm soát rủi ro đóng vai

Câu hỏi số 564281:

Vận dụng cao

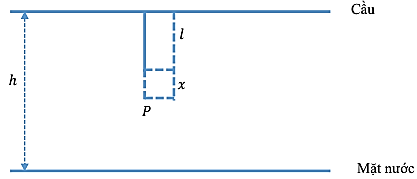
Trong các trò chơi thể thao mạo hiểm, việc ứng dụng khoa học nhằm kiểm soát rủi ro đóng vai trò quan trọng. Nhảy bungee là một trong những trò chơi như vậy. Trong trò chơi này, người chơi đứng trên cầu ở độ cao nhất định so với mặt nước. Một đầu sợi dây được buộc chặt vào thân người, đầu còn lại được cố định vào thành cầu và sau đó người chơi nhảy xuống. Để đảm bảo an toàn, chiều dài tự nhiên của sợi dây (chiều dài của sợi dây khi không co, không dãn) được chọn theo khối lượng của người chơi trước khi nhảy để khi chạm tới mặt nước thì người có tốc độ bằng không. Giả thiết rằng sợi dây có tính đàn hồi, không xoắn trong quá trình người chuyển động.

Khi người chơi có khối lượng 60kg thực hiện cú nhảy với tốc độ ban đầu không đáng kể từ vị trí có độ cao 40m so với mặt nước thì chiều dài tự nhiên của sợi dây là 20m. Bỏ qua khối lượng của dây, chiều cao của người và lực cản không khí. Gia tốc trọng trường \(g = 10m/{s^2}\).

a) Tính lực đàn hồi của sợi dây khi người ở vị trí cân bằng?

b) Tìm hệ số đàn hồi của sợi dây và tốc độ lớn nhất của người chơi đó.

c) Nếu người chơi có khối lượng 80kg thì chiều dài tự nhiên của sợi dây phải bằng bao nhiêu?

Coi rằng \(k.l = \)hằng số với k là hệ số đàn hồi và \(l\) là chiều dài tự nhiên của sợi dây.

Quảng cáo

Xem lời giải

Câu hỏi:564281

Phương pháp giải

Xác định các lực tác dụng lên vật

Viết phương trình định luật II- Niuton trong trường hợp vật cân bằng

Trọng lượng: \(P = mg\)

Cơ năng: \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}k{x^2}\)

Thế năng trọng trường: \({{\rm{W}}_t} = mgh\)

Sử dụng định luật bảo toàn cơ năng.

Tần số góc: \(\omega = \sqrt {\dfrac{k}{m}} \)

Tốc độ cực đại: \({v_{\max }} = A\omega \)

Giải chi tiết

a) Tại VTCB ta có hợp lực tác dụng lên vật: \(\overrightarrow {{F_{dh}}} + \overrightarrow P = \overrightarrow 0 \)

\( \Rightarrow {F_{dh}} = P = mg = 60.10 = 600N\)

Bỏ qua lực cản của không khí nên cơ năng được bảo toàn.

Tại điểm P ở li độ x, ta có cơ năng của vật có dạng:

\({\rm{W}} = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}k{x^2} = mg\left( {l + x} \right)\,\,\,\left( 1 \right)\)

Tại mặt nước tốc độ bằng không \(\left( {v = 0} \right)\), cơ năng tại đây:

\({\rm{W}} = \dfrac{1}{2}k{\left( {h - l} \right)^2} = mgh\,\,\,\left( 2 \right)\)

Từ (2) \( \Rightarrow \) hệ số đàn hồi của dây treo:

\(k = \dfrac{{2mgh}}{{{{\left( {h - l} \right)}^2}}} = \dfrac{{2.60.10.40}}{{{{\left( {40 - 20} \right)}^2}}} = 120N/m\)

Tìm tốc độ lớn nhất của người chơi.

Cách 1:

Tốc độ lớn nhất của người chơi đạt được khi tổng hợp lực tác dụng lên người bằng không, đó là tại VTCB

Tại VTCB, sợi dây giãn ra một đoạn:

\(x = \Delta l = \dfrac{{mg}}{k} = \dfrac{{60.10}}{{120}} = 5m\)

Thay vào (1) ta được:

\(\dfrac{1}{2}mv_{\max }^2 + \dfrac{1}{2}k\left( {\Delta {l^2}} \right) = mg\left( {l + \Delta l} \right)\)

\( \Leftrightarrow \dfrac{1}{2}.60.v_{\max }^2 + \dfrac{1}{2}{.120.5^2} = 60.10.\left( {20 + 5} \right)\)

\( \Rightarrow {v_{\max }} = 15\sqrt 2 m/s\)

Cách 2:

Từ vị trí sợi dây không co, không giãn đến ngay trước khi người chơi chạm vào mặt nước, người này dao động quanh VTCB với tần số góc:

\(\omega = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{{120}}{{60}}} = \sqrt 2 rad/s\)

Tại VTCB, sợi dây giãn ra một đoạn: \(\Delta l = \dfrac{{mg}}{k} = 5m\)

Biên độ dao động: \(A = h - l - \Delta l = 40 - 20 - 5 = 15m\)

Tốc độ lớn nhất của người chơi: \({v_{\max }} = A\omega = 15.\sqrt 2 m/s\)

c) Từ giả thuyết: \(k.l = \)hằng số

Ta có: \(k.l = {k_1}{l_1}\,\,\,\,\,\left( 3 \right)\)

Với \(k = 120N/m;l = 20m;{k_1} = \dfrac{{2{m_1}gh}}{{{{\left( {h - {l_1}} \right)}^2}}}\)

Thay vào (3) ta được: \(k.l = \dfrac{{2{m_1}gh}}{{{{\left( {h - {l_1}} \right)}^2}}}.{l_1}\)

\( \Leftrightarrow 120.20 = \dfrac{{2.80.10.40}}{{{{\left( {40 - {l_1}} \right)}^2}}}{l_1}\)

\( \Leftrightarrow l_1^2 - \dfrac{{320}}{3}{l_1} + {40^2} = 0 \Rightarrow \left[ \begin{array}{l}{l_1} = 88,61m\\{l_1} = 18,0566m\end{array} \right.\)

Với \({l_1} = 88,61m\) loại vì \({l_1} > h\) dây không có tác dụng trong trò chơi, tốc độ khi chạm nước \(v = \sqrt {2gh} > 0\), vi phạm giả thiết đề bài đã cho là bằng 0.

Với \({l_1} = 18,0566m\) thỏa mãn điều kiện.

Vậy với người chơi 80kg, chiều dài tự nhiên của dây cần được chọn là 18,0566m để tốc độ của người chơi bằng 0 khi chạm tới mặt nước.

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.