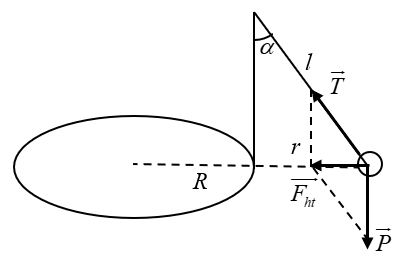
Một vật được treo vào đầu một chiếc cọc cắm thẳng đứng ở mép một chiếc đĩa tròn
Một vật được treo vào đầu một chiếc cọc cắm thẳng đứng ở mép một chiếc đĩa tròn nằm ngang bằng một sợi dây dài l = 0,1m. Khi đĩa quay với vận tốc góc 1 vòng/s thì thấy dây lệch đi một góc \(\alpha = {30^0}\) khỏi phương thẳng đứng. Hãy tính bán kính của đĩa. Lấy \(g = 10\,\,m/{s^2}\).
Đáp án đúng là: B
Quảng cáo
Gia tốc hướng tâm: \({a_{ht}} = {\omega ^2}r\)
Sử dụng phương pháp động lực học
Tốc độ góc của đĩa là:
\(\omega = 1\,\,\left( {vong/s} \right) = 2\pi \,\,\left( {rad/s} \right)\)
Bán kính quỹ đạo của vật là:
\({r_v} = r + R = l\sin \alpha + R\)
Gia tốc hướng tâm:
\({a_{ht}} = {\omega ^2}{r_v} = {\omega ^2}\left( {l\sin \alpha + R} \right)\)
Áp dụng định luật II Newton, ta có:
\(\overrightarrow P + \overrightarrow T = \overrightarrow {{F_{ht}}} \)
Từ hình vẽ ta có:
\(\begin{array}{l}{F_{ht}} = P\tan \alpha \Rightarrow m{a_{ht}} = mg\tan \alpha \Rightarrow {a_{ht}} = g\tan \alpha \\ \Rightarrow {\omega ^2}\left( {l\sin \alpha + R} \right) = g\tan \alpha \\ \Rightarrow 4{\pi ^2}.\left( {0,1.\sin {{30}^0} + R} \right) = 10.\tan {30^0}\\ \Rightarrow R \approx 0,096\,\,\left( m \right) = 9,6\,\,\left( {cm} \right)\end{array}\)
Đáp án cần chọn là: B
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
