Tam giác ABC có \(M\) trên cạnh AC. Kẻ \(MN//BC(N\) thuộc \(AB),MP//AB(P\) thuộc \(BC)\). Biết diện

Câu hỏi số 656843:

Thông hiểu

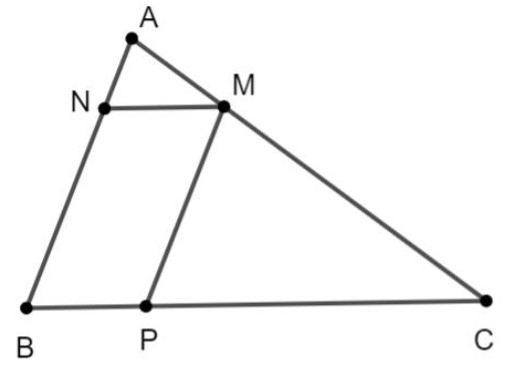
Tam giác ABC có \(M\) trên cạnh AC. Kẻ \(MN//BC(N\) thuộc \(AB),MP//AB(P\) thuộc \(BC)\). Biết diện tích 2 tam giác AMN và CMP lần lượt là \(4\;{\rm{c}}{{\rm{m}}^2}\) và \(9\;{\rm{c}}{{\rm{m}}^2}\).

a) Chứng minh 2 tam giác \({\rm{AMN}}\) và \({\rm{CMP}}\) đồng dạng. Tính tỉ số \(\dfrac{{AM}}{{MC}}\)

b) Tính diện tích tam giác \({\rm{ABC}}\)

Quảng cáo

Xem lời giải

Câu hỏi:656843

Phương pháp giải

a) Chứng minh 2 tam giác \({\rm{AMN}}\) và \({\rm{CMP}}\) đồng dạng theo trường hợp g – g.

Suy ra tỉ số diện tích \(\dfrac{{{{\rm{S}}_{{\rm{AMN}}}}}}{{{{\rm{S}}_{{\rm{MCP}}}}}} = {\left( {\dfrac{{{\rm{AM}}}}{{{\rm{MC}}}}} \right)^2}\) để tính \(\dfrac{{AM}}{{MC}}\)

b) Chứng minh 2 tam giác ABC và ANM đồng dạng theo trường hợp g – g.

Suy ra tỉ số diện tích \(\dfrac{{{{\rm{S}}_{{\rm{ABC}}}}}}{{{{\rm{S}}_{{\rm{ANM}}}}}} = {\left( {\dfrac{{{\rm{AC}}}}{{{\rm{AM}}}}} \right)^2}\) để tích được diện tích tam giác ABC.

Giải chi tiết

a) Xét \(\Delta {\rm{AMN}}\) và \(\Delta {\rm{MCP}}\) có:

\(\begin{array}{l}\angle {\rm{NAM}} = \angle {\rm{PMC}}(MP\parallel AB)\\\angle {\rm{AMN}} = \angle {\rm{MCP}}(MN\parallel BC)\\ \Rightarrow \Delta {\rm{AMN}}\backsim\Delta {\rm{MCP}}({\rm{g}}.{\rm{g}})\\ \Rightarrow \dfrac{{{{\rm{S}}_{{\rm{AMN}}}}}}{{{{\rm{S}}_{{\rm{MCP}}}}}} = {\left( {\dfrac{{{\rm{AM}}}}{{{\rm{MC}}}}} \right)^2} = \dfrac{4}{9}\\ \Rightarrow \dfrac{{{\rm{AM}}}}{{{\rm{MC}}}} = \dfrac{2}{3}\end{array}\)

b) Có: \(\dfrac{{AM}}{{MC}} = \dfrac{2}{3} \Rightarrow \dfrac{{AM}}{{AC}} = \dfrac{2}{5} \Rightarrow \dfrac{{AC}}{{AM}} = \dfrac{5}{2}\)

Xét \(\Delta {\rm{ABC}}\) và \(\Delta {\rm{ANM}}\) có:

\(\left\{ \begin{array}{l}\angle {\rm{ANM}} = \angle {\rm{ABC}}\\\angle {\rm{AMN}} = \angle {\rm{ACB}}\end{array} \right.(MN\parallel BC)\)

\(\begin{array}{l} \Rightarrow \Delta {\rm{ABC}} \backsim \Delta {\rm{ANM}}({\rm{g - g}})\\ \Rightarrow \dfrac{{{{\rm{S}}_{{\rm{ABC}}}}}}{{{{\rm{S}}_{{\rm{ANM}}}}}} = {\left( {\dfrac{{{\rm{AC}}}}{{{\rm{AM}}}}} \right)^2}\\ \Rightarrow \dfrac{{{S_{ABC}}}}{4} = \dfrac{{25}}{4} \Rightarrow {S_{ABC}} = 25\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\end{array}\)

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link