Một con lắc lò xo treo thẳng đứng gồm lò xo nhẹ có độ cứng k = 50N/m và vật M khối lượng
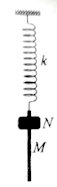
Một con lắc lò xo treo thẳng đứng gồm lò xo nhẹ có độ cứng k = 50N/m và vật M khối lượng 200g có dạng một thanh trụ dài. Vật N được lồng bên ngoài vật M như hình bên. Nâng hai vật lên đến vị trí lò xo không biến dạng rồi thả N để N trượt thẳng đứng xuống dọc theo M, sau đó thả nhẹ M. Sau khi thả M một khoảng thời gian \(\dfrac{2}{{15}}s\)thì N rời khỏi M. Biết rằng trước khi rời khỏi M thì N luôn trượt xuống so với M và lực ma sát giữa chúng có độ lớn không đổi và bằng 0,5N. Bỏ qua lực cản không khí. Lấy g = 10m/s2 và \({\pi ^2} = 10\). Sau khi N rời khỏi M, M dao động điều hòa, độ biến dạng cực đại của lò xo là \(\Delta {l_{\max }}\). Giá trị \(\Delta {l_{\max }}\) gần nhất với giá trị nào sau đây?
Đáp án đúng là: D
Quảng cáo
Sử dụng lý thuyết về dao động điều hòa của lò xo.
Công thức độc lập thời gian.
+ Khi N trượt:
* Vị trí cân bằng của M là O1, độ dãn của lò xo là \(\Delta {l_{01}}\)
Với \(\Delta {l_{01}} = \dfrac{{mg + {F_{ms}}}}{k} = 0,05\,m\, = 5\,cm\)
* Tần số góc \(\omega = \sqrt {\dfrac{k}{m}} = 5\pi (rad/s)\) (do M không nối cứng với N)
* Biên độ dao động là A1 = 5 cm
+ Sau thời gian \(\dfrac{2}{{15}}\)s kể từ biên âm, vật tới vị trí:
\({x_1} = - {A_1}\cos \left( {\omega t} \right) = - 0,05\cos \left( {5\pi .\dfrac{2}{{15}}} \right) = 2,5\,cm\)
Hay O1M = 2,5cm
+ Khi N rời khỏi M, M có vị trí cân bằng O, ứng với độ biến dạng của lò xo là:
\(\Delta {l_0} = \dfrac{{mg}}{k} = 0,04\,m = 4\,cm\)
M có vị trí so với O là \({x_{01}} = {O_1}M + O{O_1} = 2,5 + \left( {5 - 4} \right) = 3,5\left( {cm} \right)\)
Tần số góc \(\omega = \sqrt {\dfrac{k}{m}} = 5\pi \)(rad/s)
Áp dụng công thức độc lập thời gian tại M, có:
\(\begin{array}{l}
{v^2} = {\omega ^2}\left( {{A^2} - {x^2}} \right) = {\omega ^2}\left( {A_1^2 - x_1^2} \right)\\
\Leftrightarrow {A^2} - 3,{5^2} = {5^2} - 2,{5^2} \approx 5,57(cm)
\end{array}\)
+ Khi vật xuống tới vị trí biên dưới thì độ biến dạng của lò xo là lớn nhất:
\(\Delta {l_{\max }} = \Delta {l_0} + A = 4 + 5,57 = 9,57cm\)
Đáp án cần chọn là: D
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
