Sóng ngang truyền trên mặt chất lỏng với tốc độ 3 cm/s. Xét hai phần tử M và N nằm trên một

Câu hỏi số 665210:

Vận dụng cao

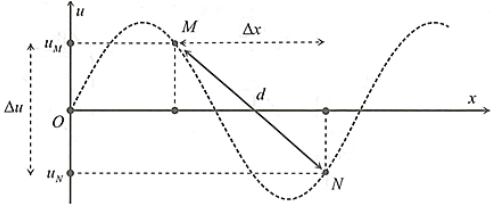
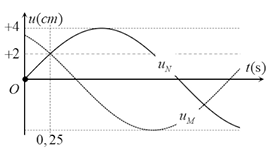
Sóng ngang truyền trên mặt chất lỏng với tốc độ 3 cm/s. Xét hai phần tử M và N nằm trên một phương truyền sóng có vị trí cân bằng cách nhau một khoảng nhỏ hơn bước sóng. Đồ thị biểu diễn li độ sóng của M và N theo thời gian t như hình vẽ. Khoảng cách giữa hai phần tử chất lỏng tại M và N vào thời điểm t = 2,25s là

A. 61,18 mm.

B. 30,90 mm.

C. 30,59 mm.

D. 61,84 mm.

Đáp án đúng là: C

Quảng cáo

Xem lời giải

Câu hỏi:665210

Phương pháp giải

Đọc đồ thị u-t

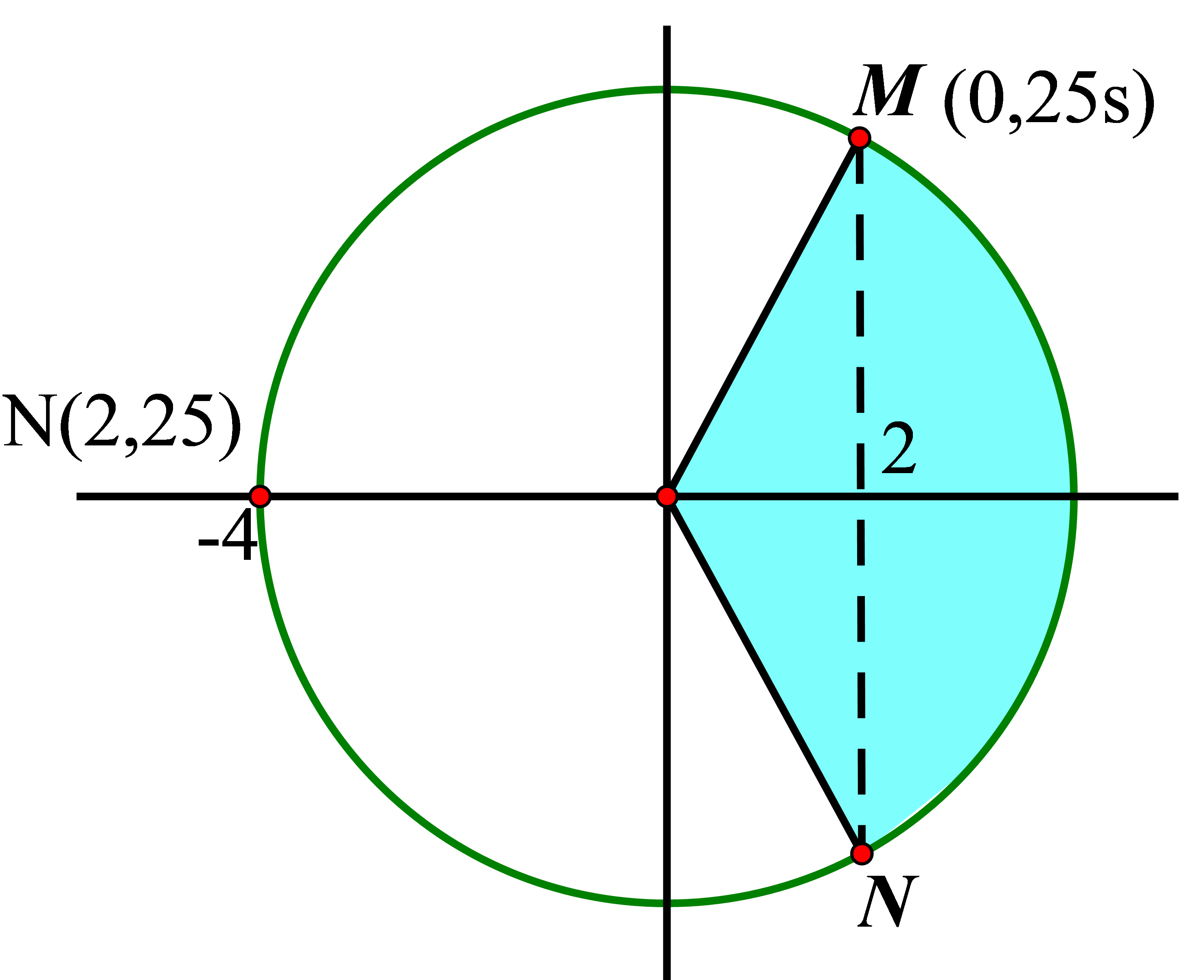
Sử dụng VTLG và công thức tính góc quét: \(\Delta \varphi = \omega .\Delta t\)

Bước sóng: \(\lambda = vT = \dfrac{v}{f}\)

Độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi .\Delta x}}{\lambda }\)

Công thức tính khoảng cách: \(d = \sqrt {d_0^2 + \Delta {u^2}} \)

Giải chi tiết

Từ đồ thị ta có tại t = 0,25 s, M đi qua vị trí có li độ \(u = 2\,\,cm = \dfrac{A}{2}\) theo chiều âm và điểm N đi qua vị trí \(u = 2\,\,cm = \dfrac{A}{2}\) theo chiều dương. Biễu diễn các vị trí tương ứng trên đường tròn ta có:

Từ vòng tròn, xác định được độ lệch pha giữa M và N là: \(\Delta {\varphi _{MN}} = \dfrac{{2\pi }}{3}\)

Khoảng thời gian N dao động từ N (t=0) đến N(t=0,25 s) là:

\(t = \dfrac{\alpha }{\omega } = \dfrac{\pi }{6} \cdot \dfrac{T}{{2\pi }} \Leftrightarrow \dfrac{T}{{12}} = 0,25\,\,\left( s \right) \Rightarrow T = 3\,\,\left( s \right)\)

Bước sóng:

\(\lambda = v.T = 3.3 = 9\,\,\left( {cm} \right)\)

Mặt khác, ta có:

\(\left[ \begin{array}{l}\Delta {\varphi _{MN}} = \dfrac{{2\pi }}{3} = \dfrac{{2\pi .x}}{\lambda }\\\Delta {\varphi _{MN}} = \dfrac{{4\pi }}{3} = \dfrac{{2\pi .x}}{\lambda }\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = \dfrac{\lambda }{3} = \dfrac{9}{3} = 3cm\\x = \dfrac{{2\lambda }}{3} = 6cm\end{array} \right.\)

Chính là khoảng cách theo không gian tại vị trí cân bằng của M và N.

Trong khoảng thời gian từ t = 0,25 s đến t = 2,25 s ta có \(\Delta t = 2\,\,\left( s \right) = \dfrac{{2T}}{3}\) tương ứng với góc quét:

\(\alpha = \omega .\Delta t = \dfrac{{2\pi }}{T} \cdot \dfrac{{2T}}{3} = \dfrac{{4\pi }}{3}\)

→ Tại thời điểm t = 2,25 s có N đi qua vị trí biên âm \({u_N} = - A = - 4\,\,mm\) và M đi qua vị trí \({u_M} = \dfrac{A}{2} = 2\,\,mm\) theo chiều dương.

\( \Rightarrow \Delta u = {u_M} - {u_N} = 2 - ( - 4) = 6\,\,\left( {mm} \right)\)

Khoảng cách giữa M và N khi đó:

\(d = \sqrt {\Delta {u^2} + {x^2}} = \sqrt {{6^2} + {{30}^2}} = 30,59\;\left( {mm} \right)\)

Hoặc \(d = \sqrt {\Delta {u^2} + {x^2}} = \sqrt {{6^2} + {{60}^2}} = 60,3\left( {mm} \right)\)

Đáp án cần chọn là: C

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.