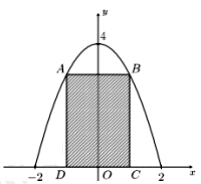
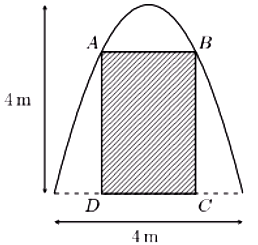
Trong đợt hội trại " Khi tôi 18 " được tổ chức tại trường THPT \(X\), Đoàn trường
Trong đợt hội trại " Khi tôi 18 " được tổ chức tại trường THPT \(X\), Đoàn trường có thực hiện một dự án ảnh trưng bầy trên một pano có dạng Parabol như hình vẽ. Biết rằng Đoàn trường sẽ yêu cầu các lớp gửi hình dự thi và dán lên khu vực hình chữ nhật \(ABCD\). Phần còn lại sẽ trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là 200.000 đồng cho một \({m^2}\) bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu (làm tròn đến hàng phần nghìn)?
Đáp án đúng là: D
Quảng cáo
Gắn hệ trục toạ độ, xác định toạ độ các điểm và các hàm số từ đó tính diện tích bằng tích phân
Xét hệ trục tọa độ như hình vẽ. Parabol của pano có dạng $y=a x^2+c(a<0)$.
Vì $(P)$ cắt $O y$ tại điểm có tung độ 4 nên $c=4$.
Mà $(P)$ đi qua điểm $(2 ; 0)$ nên $a=-1$.
Như vậy Parabol của pano có phương trình $y=4-x^2$ trên đoạn $[-2 ; 2]$.
Già sừ $C D=2 x$ với $0 \leq x \leq 2$.
Khi đó diện tích của hình chữ nhật là $S_{A B C D}=2 x\left(4-x^2\right)$.
Diện tích phần trang trí của hoa văn là
$S(x)=\int_{-2}^2\left(4-x^2\right) \mathrm{d} x-2 x\left(4-x^2\right)=2 x^3-8 x+\dfrac{32}{3}$
Hàm số $S(x)$ có $S^{\prime}(x)=6 x^2-8$ và $S^{\prime}(x)=0 \Leftrightarrow x= \pm \dfrac{2 \sqrt{3}}{3}$
Trên đoạn $[-2 ; 2]$ ta có $S( \pm 2)=\dfrac{32}{3} ; S\left(\dfrac{2 \sqrt{3}}{3}\right)=\dfrac{96-32 \sqrt{3}}{9} ; S\left(-\dfrac{2 \sqrt{3}}{3}\right)=\dfrac{96+32 \sqrt{3}}{9}$
Do đó giá trị nhỏ nhất của $S(x)$ trên đoạn $[-2 ; 2]$ là $\dfrac{96-32 \sqrt{3}}{9}$
Chi phí cho họa tiết văn hoa lúc đó là $\dfrac{96-32 \sqrt{3}}{9} \times 200.000 \approx 902.000$ đồng.
Đáp án cần chọn là: D
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
