Đánh giá năng lực Hà Nội
Đánh giá năng lực Hà Nội
Cho tam giác ABC có diện tích bằng 90 cm2. Trên cạnh AC lấy điểm M sao cho AM = 2 MC. Lấy I là trung điểm của BM. Kéo dài AI cắt BC tại K.
a) Tính diện tích tam giác BMC.
b) Tính tỉ số diện tích hai tam giác ABI và BIC
c) So sánh \(\dfrac{{BK}}{{KC}}\)
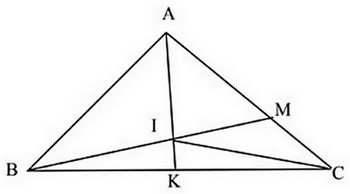
Câu 686304: Cho tam giác ABC có diện tích bằng 90 cm2. Trên cạnh AC lấy điểm M sao cho AM = 2 MC. Lấy I là trung điểm của BM. Kéo dài AI cắt BC tại K.
a) Tính diện tích tam giác BMC.
b) Tính tỉ số diện tích hai tam giác ABI và BIC
c) So sánh \(\dfrac{{BK}}{{KC}}\)
Quảng cáo
a) SBMC = \(\dfrac{1}{3}\)SABC (Chung đường cao hạ từ B và đáy MC = \(\dfrac{1}{3}\) AC).
b) Dựa vào các tam giác có chung đường cao để suy luận.
c) Dựa vào các tam giác có chung đường cao để tìm được tỉ số.
-
Giải chi tiết:
a) SBMC = \(\dfrac{1}{3}\)SABC (Chung đường cao hạ từ B và đáy MC = \(\dfrac{1}{3}\) AC)
\( \Rightarrow \)SBMC = \(90 \times \dfrac{1}{3} = 30\) (cm2)
b) Nối IC ta có:
SABM = 2 x SBMC (Chung chiều cao hạ từ B và đấy AM = 2 x MC)
\( \Rightarrow \)Chiều cao hạ từ A xuống BM gấp 2 lần chiều cao hạ từ C xuống đáy BM
\( \Rightarrow \)SABI = 2 x SBIC (Chung đáy BI và chiều cao hạ từ A xuống BM gấp 2 lần chiều cao hạ từ C xuống đáy BM)
c) SABI = SAIM (Chung chiều cao hạ từ A và đáy BI = IM)
Mà SAIM = \(\dfrac{2}{3}\) SAIC (Chung đường cao hạ từ I và đáy AM = \(\dfrac{2}{3}\) AC)
\( \Rightarrow \)SABI = SAIC
\( \Rightarrow \) Đường cao hạ từ B xuống AI = \(\dfrac{2}{3}\) đường cao từ C xuống AI
\( \Rightarrow \)SBAK = \(\dfrac{2}{3}\)SCAK (Chung đáy AK và đường cao hạ từ B xuống AK = \(\dfrac{2}{3}\) đường cao từ C xuống AK)
\( \Rightarrow \)BK = \(\dfrac{2}{3}\) CK
Lời giải sai Bình thường Khá hay Rất Hay
Tham Gia Group Dành Cho 2K14 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến các môn Toán, Tiếng Việt, Tiếng Anh lớp 5 trên Tuyensinh247.com cam kết giúp con lớp 5 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
