Làm 1) Đà Nẵng có rất nhiều điểm đến độc đáo điển hình như cầu Rồng, cầu quay sông

Câu hỏi số 724141:

Vận dụng cao

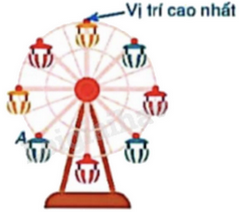
Làm 1) Đà Nẵng có rất nhiều điểm đến độc đáo điển hình như cầu Rồng, cầu quay sông Hàn hay khu du lịch Bà Nà Hills… Bên cạnh đó không thể không kể tới vòng quay mặt trời Sun Wheel – điểm “check-in” quen thuộc của giới trẻ Đà thành. Cho vòng quay mặt trời gồm tám cabin như hình bên. Hỏi để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều kim đồng hồ quanh tâm bao nhiêu độ?

2) Cho 51 số nguyên dương đôi một khác nhau không vượt quá 100. Chứng minh rằng tồn tại hai số trong số 51 số nguyên dương đó có tổng bằng 101.

Quảng cáo

Xem lời giải

Câu hỏi:724141

Phương pháp giải

Giải chi tiết

1) Chia đường tròn thành 8 tám hình quạt bằng nhau (mỗi hình quạt tạo bởi 2 cabin)

Góc tạo bởi 2 cabin là \(360^\circ :8 = 45^\circ \)

Cabin A cách vị trí cao nhất 3 hình quạt (theo chiều kim đồng hồ)

Như vậy để di chuyển đến vị trí cao nhất thì cabin A cần di chuyển \(3.45^\circ = 135^\circ \) quanh tâm

2) Gọi 51 số nguyên dương đã cho lần lượt là \({a_1},\,\,{a_2}, \ldots ,\,\,{a_{51}}\,\,\left( {0 < {a_i} < 101,\,\,i = \overline {1,51} } \right)\)

Không mất tính tổng quát giả sử \(0 < {a_1} < {a_2} < \ldots < {a_{51}} < 101\)

Xét 51 số nguyên dương \(101 - {a_1},\,\,101 - {a_2}, \ldots ,101 - {a_{51}}\)

Từ giả thiết trên ta suy ra \(0 < 101 - {a_{51}} < \ldots < 101 - {a_2} < 101 - {a_1} < 101\)

Như vậy 102 số nguyên dương trên \({a_1},\,\,{a_2}, \ldots ,{a_{51}},\,\,101 - {a_1},101 - {a_2}, \ldots ,101 - {a_{51}}\) đều nằm trong 100 số nguyên dương \(1,\,\,2, \ldots ,100\)

Suy ra trong 102 số đó phải có ít nhất 2 số bằng nhau (2 số thuộc hai nhóm khác nhau)

Gọi 2 số thỏa mãn là \({a_m}\) và \(101 - {a_n}\) (\(1 \le m,n \le 51\))

Rõ ràng \(m \ne n\) vì nếu \(m = n\) thì \({a_m} = 101 - {a_m} \Rightarrow 2{a_m} = 101\) (vô lí)

Như vậy \({a_m} = 101 - {a_n} \Rightarrow {a_m} + {a_n} = 101\) (đpcm)

PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link