Tại hai điểm A và B của tam giác ABC ở mặt nước phẳng lặng nằm ngang có hai nguồn kết hợp

Câu hỏi số 741380:

Vận dụng

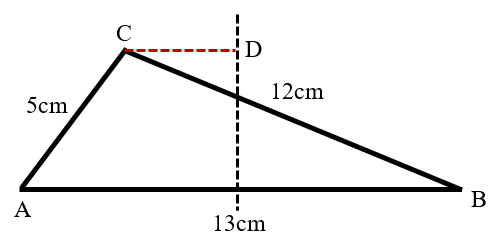
Tại hai điểm A và B của tam giác ABC ở mặt nước phẳng lặng nằm ngang có hai nguồn kết hợp cùng biên độ và cùng pha với bước sóng 1,6 cm. Cho biết AB = 13 cm; AC = 5,0 cm; BC = 12 cm. Coi sóng mặt nước là sóng ngang và biên độ sóng không giảm khi lan truyền.

1. Tính số vân giao thoa cực đại trên mặt nước.

2. Trong khoảng giữa C và đường trung trực của AB ở mặt nước có mấy vân giao thoa cực tiểu?

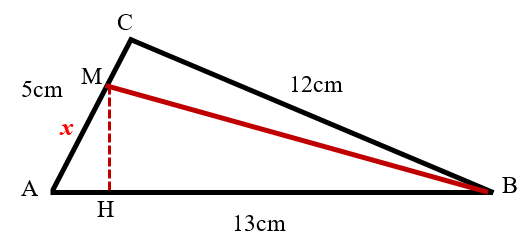
3. M là điểm cực đại trên cạnh CA và gần C nhất. Tính khoảng cách MA.

Quảng cáo

Xem lời giải

Câu hỏi:741380

Phương pháp giải

- Trong giao thoa sóng hai nguồn cùng pha:

+ Điều kiện có cực đại giao thoa: \({d_2} - {d_1} = k\lambda \)

+ Điều kiện có cực tiểu giao thoa: \({d_2} - {d_1} = \left( {k + \dfrac{1}{2}} \right)\lambda \)

- Sử dụng kiến thức hình học.

Giải chi tiết

1. Điều kiện có cực đại giao thoa:

\({d_2} - {d_1} = k\lambda = 1,6.k\)

Số vân giao thoa cực đại trên mặt nước bằng số giá trị k nguyên thỏa mãn:

\(\begin{array}{l} - AB < {d_2} - {d_1} < AB \Leftrightarrow - 13 < 1,6k < 13\\ \Leftrightarrow - 8,125 < k < 8,125 \Rightarrow k = - 8; - 7;..;8\end{array}\)

Có 17 giá trị của k thỏa mãn → có 17 vân giao thoa cực đại trên mặt nước.

2. Điều kiện có cực tiểu giao thoa: \({d_2} - {d_1} = \left( {k + \dfrac{1}{2}} \right)\lambda = 1,6.\left( {k + \dfrac{1}{2}} \right)\)

Số vân giao thoa cực tiểu trong khoảng giữa C và đường trung trực của AB bằng số giá trị k nguyên thỏa mãn:

\(\begin{array}{l}0 < {d_2} - {d_1} < BC - AC \Leftrightarrow 0 < 1,6.\left( {k + \dfrac{1}{2}} \right) < 7\\ \Leftrightarrow - 0,5 < k < 3,875 \Rightarrow k = 0;1;2;3\end{array}\)

Có 4 giá trị của k thỏa mãn → có 4 vân giao thoa cực tiểu trong khoảng giữa C và đường trung trực của AB.

3. Tại C có:

\(\left\{ \begin{array}{l}AC = 5cm\\BC = 12cm\end{array} \right. \Rightarrow \dfrac{{BC - AC}}{\lambda } = \dfrac{{12 - 5}}{{1,6}} = 4,375\)

M là điểm cực đại trên cạnh CA và gần C nhất → M thuộc cực đại ứng với k = 5

\( \Rightarrow BM - AM = 5\lambda = 5.1,6 \Rightarrow BM - AM = 8\left( {cm} \right)\,\,\,\left( 1 \right)\)

Đặt \(AM = x\,\,\,\,\left( 2 \right)\)

Xét tam giác ABC có: \(\left\{ \begin{array}{l}BC = 12cm\\AC = 5cm\\AB = 13cm\end{array} \right.\)

Ta thấy: \(A{B^2} = A{C^2} + B{C^2} \Rightarrow \Delta ABC\) vuông tại C.

\( \Rightarrow \Delta MHA \sim \Delta BCA\left( {g - g} \right) \Rightarrow \dfrac{{MH}}{{BC}} = \dfrac{{MA}}{{BA}} = \dfrac{{HA}}{{CA}}\)

\( \Leftrightarrow \dfrac{{MH}}{{12}} = \dfrac{x}{{13}} = \dfrac{{HA}}{5} \Rightarrow \left\{ \begin{array}{l}MH = \dfrac{{12x}}{{13}}\\HA = \dfrac{{5x}}{{13}}\end{array} \right.\)

\( \Rightarrow BH = 13 - AH = 13 - \dfrac{{5x}}{{13}}\)

Áp dụng định lí Pitago cho tam giác vuông MHB có:

\(\begin{array}{l}BM = \sqrt {M{H^2} + H{B^2}} = \sqrt {{{\left( {\dfrac{{12x}}{{13}}} \right)}^2} + {{\left( {13 - \dfrac{{5x}}{{13}}} \right)}^2}} \\ \Rightarrow BM = \sqrt {{x^2} - 10x + 169} \,\,\,\,\left( 3 \right)\end{array}\)

Thay (2) và (3) vào (1) ta được:

\(\begin{array}{l}\sqrt {{x^2} - 10x + 169} - x = 8 \Leftrightarrow {x^2} - 10x + 169 = {\left( {8 + x} \right)^2}\\ \Leftrightarrow {x^2} - 10x + 169 = 64 + 16x + {x^2}\\ \Leftrightarrow 26x = 105 \Rightarrow x \approx 4,04\left( {cm} \right) \Rightarrow MA = 4,04\left( {cm} \right)\end{array}\)

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.