Bạn Hoa thường đi bơi ở hồ bơi Sky Garden cạnh nhà, hồ bơi có thiết kế là

Câu hỏi số 757292:

Vận dụng

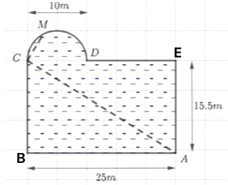
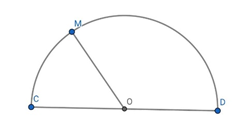
Bạn Hoa thường đi bơi ở hồ bơi Sky Garden cạnh nhà, hồ bơi có thiết kế là một hình chữ nhật với chiều dài \(25\;m\), chiều rộng \(15,5\;m\) và bên cạnh đó có một hồ bán nguyệt đường kính \(10\;m\)( tham khảo hình vẽ 1). Trong một lần bể bơi vắng người nên Hoa đã thực hiện một chu trình là bơi theo đoạn thẳng \(AC\) rồi bơi tiếp theo đoạn thẳng \(CM\) , với \(M\) là một vị trí bất kì trên hình bán nguyệt. Ngay sau đó bạn đi bộ theo một hướng qua điểm \(D\) dọc bờ của hồ bơi để quay lại vị trí \(A\) và kết thúc chu trình. (tham khảo hình vẽ 2).

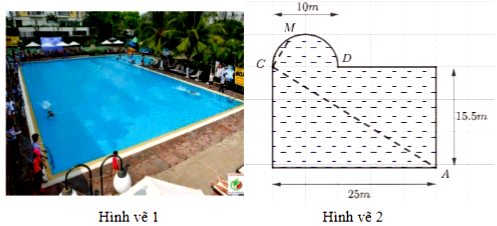
Biết rằng vận tốc bơi của Hoa là \(2,4\;km/h\), vận tốc đi bộ là \(4,8\;km/h\) và tốc độ bơi, vận tốc đi bộ không thay đổi trong một chu trình. Hỏi thời gian chậm nhất để Hoa thực hiện xong chu trình trên là bao nhiêu phút? (kết quả làm tròn đến hàng phần chục)

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:757292

Phương pháp giải

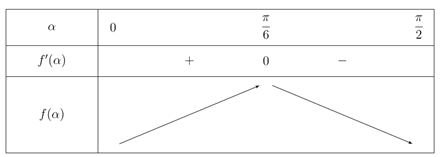
Biểu diễn thời gian Hoa thực hiện xong chu trình theo hàm số và tìm giá trị lớn nhất của hàm đó

Giải chi tiết

Đổi \(2,4km/h = \dfrac{2}{3}m/s\) và \(4,8km/h = \dfrac{4}{3}m/s.\)

Quãng đường mà bạn Hoa phải đi để hoàn thành chu trình là

\(A C+C M+\overparen{M D}+D E+E A\)

Biết vận tốc bơi và đi bộ của Hoa là không đổi, do đó thời gian để Hoa hoàn thành chu trình là

\(\dfrac{A C}{2/3}+\dfrac{C M}{2/3}+\dfrac{\overparen{M D}}{4/3}+\dfrac{D E}{4/3}+\dfrac{E A}{4/3}\)

Vì độ dài \(AC,DE,EA\) là không đổi.

Suy ra, để thời gian hoàn thành chu trình là chậm thì \(\dfrac{C M}{2/3}+\dfrac{\overparen{M D}}{4/3}\) là lớn nhất.

Xét nửa đường tròn đường kính \(C D=10 \mathrm{~m}\) có tâm \(O\):

Điểm \(M\) thuộc nửa đường tròn nên tam giác \(M C D\) vuông tại \(M\).

Đặt \(\alpha=\widehat{M C D} \Rightarrow \widehat{M O D}=2 \alpha\).

Ta tính được \(CM=10 \cos \alpha\); \(\overparen{MD}=10 \alpha\).

\(\dfrac{C M}{2/3}+\dfrac{\overparen{M D}}{4/3}=\dfrac{10 \cos \alpha}{2/3}+\dfrac{10 \alpha}{4/3}=\dfrac{10}{4/3}(2 \cos \alpha+\alpha)\)

Xét hàm số \(f(\alpha)=2 \cos \alpha+\alpha\)

Có \(f^{\prime}(x)=-\sin \alpha+1=0\) mà \(\alpha \in\left[0 ; \dfrac{\pi}{2}\right] \Rightarrow x=\dfrac{\pi}{6}\).

Ta có bảng biến thiên hàm \(f(\alpha)\).

Từ bảng biến thiên ta có

\(\max _{\alpha \in\left[0 ; \dfrac{\pi}{2}\right]} f(\alpha)=f\left(\dfrac{\pi}{6}\right)=\sqrt{3}+\dfrac{\pi}{6}\).

\(\Rightarrow\left(\dfrac{C M}{2/3}+\dfrac{\overparen{M D}}{4 / 3}\right)_{\max }=\dfrac{10}{4/3} \cdot\left(\sqrt{3}+\dfrac{\pi}{6}\right)\)

Ta có \(A C=\sqrt{25^2+15,5^2}\); \(D E=15\); \(E A=15,5\).

Thời gian hoàn thành chu trình chậm nhất là

\(\dfrac{\sqrt{25^2+15,5^2}}{2/3}+\dfrac{10}{4/ 3} \cdot\left(\sqrt{3}+\dfrac{\pi}{6}\right)+\dfrac{15}{4/ 3}+\dfrac{15,5}{4/3} \approx 83,9\) (giây)

Có 83,9 giây \(\approx 1,4\) phút.
Vậy thời gian chậm nhất để Hoa hoàn thành chu trình là 1,4 phút.

Đáp án cần điền là: 1,4

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.