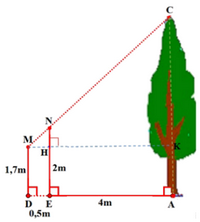
a) Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao 2m và đặt xa
a) Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao 2m và đặt xa cây 4m. Sau khi người ấy lùi ra xa cách cọc 0,5m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng (như hình vẽ). Hỏi cây cao bao nhiêu, biết khoảng cách từ chân đến mắt người ấy là 1,7m
b) Cho \(x,\,\,y > 0\) và \(x + y \ge 3\). Tìm giá trị nhỏ nhất của \(A = 3x + 2y + \dfrac{2}{x} + \dfrac{4}{y}\)
Quảng cáo
a) Dựa vào tam giác đồng dạng để suy ra các cặp cạnh tỉ lệ và tính toán.
b) Phân tích \(A = 3x + 2y + \dfrac{2}{x} + \dfrac{4}{y} = \left( {x + y} \right) + \left( {2x + \dfrac{2}{x}} \right) + \left( {y + \dfrac{4}{y}} \right)\) và đưa về các hằng đẳng thức để tìm giá trị nhỏ nhất.
a)
Ta có: \(MH = DE = 0,5m;\,\,HK = EA = 4m\)
Nên \(MK = MH + HK = 0,5 + 4 = 4,5\left( m \right)\)
Lại có: \(KA = HE = MD = 1,7m;\,\,NE = 2m\)
Nên \(NH = NE - HE = 2 - 1,7 = 0,3m\)
Xét \(\Delta HMN\) và \(\Delta KMC\) có:
\(\angle NHM = \angle CKM = 90^\circ \)
\(\angle HMN\,\,chung\)
\( \Rightarrow \Delta HMN\)~\(\Delta KMC\,\,\left( {g.g} \right)\)
\( \Rightarrow \dfrac{{HM}}{{KM}} = \dfrac{{NH}}{{KC}} \Rightarrow CK = \dfrac{{KM.NH}}{{HM}} = \dfrac{{4,5.0,3}}{{0,5}} = 2,7\)
Do đó \(CA = CK + KA = 2,7 + 1,7 = 4,4\)
Vậy chiều cao của cái cây là \(4,4m\)
b) Ta có:
\(A = 3x + 2y + \dfrac{2}{x} + \dfrac{4}{y} = \left( {x + y} \right) + \left( {2x + \dfrac{2}{x}} \right) + \left( {y + \dfrac{4}{y}} \right)\)
\( = \left( {x + y - 3} \right) + \left( {2x + \dfrac{2}{x} - 4} \right) + \left( {y + \dfrac{4}{y} - 4} \right) + 11\)
\( = \left( {x + y - 3} \right) + \dfrac{{2{{\left( {x - 1} \right)}^2}}}{x} + \dfrac{{{{\left( {y - 2} \right)}^2}}}{y} + 11 \ge 11,\,\,\forall x,y \in \mathbb{R}\)
Dấu “=” xảy ra khi và chỉ khi \(x = 1,\,\,y = 2\)
Vậy giá trị nhỏ nhất của \(A\) bằng 11 khi \(x = 1,\,\,y = 2\)
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
