1) Một cái thùng dùng để đựng gạo có dạng nửa hình cầu với đường kính \(50cm\), phần

Câu hỏi số 765231:

Vận dụng

1) Một cái thùng dùng để đựng gạo có dạng nửa hình cầu với đường kính \(50cm\), phần gạo vun lên có dạng hình nón cao \(12cm\).

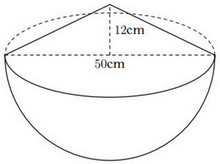
a) Tính thể tích phần gạo trong thùng.

b) Nhà bạn An dùng lon sữa bò dạng hình trụ với bán kính đáy là\(5cm\), chiều cao \(14cm\) dùng để đong gạo mỗi ngày. Biết rằng mỗi ngày nhà An ăn 4 lon gạo và mỗi lần đong thì lượng gạo chiếm \(90\% \) thể tích của lon. Hỏi cần ít nhất bao nhiêu ngày để nhà An có thể ăn hết số gạo trong thùng?

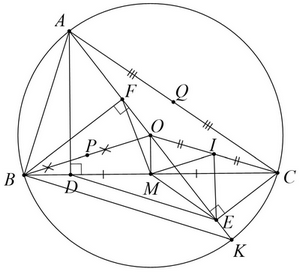
2) Cho đường tròn tâm \((O)\) và dây \(BC\) cố định không đi qua \(O\). Trên cung lớn \(BC\) lấy điểm \(A\) sao cho \(AB < AC\). Kẻ đường kính \(AK,E\) là hình chiếu của \(C\) trên \(AK\). \(M\) là trung điểm của \(BC\).

a) Chứng minh bốn \(C,\,E,\,\,M,\,O\)cùng thuộc một đường tròn.

b) Kẻ \(AD \bot BC\) tại \(D\). Chứng minh \(AD.AK = AB.AC\) và \(\Delta MDE\) cân.

c) Gọi \(F\) là hình chiếu của \(B\) trên \(AK\). Chứng minh khi di chuyển trên cung lớn \(BC\) thì tâm đường tròn ngoại tiếp \(\Delta DEF\) là 1 điểm cố định.

Quảng cáo

Xem lời giải

Câu hỏi:765231

Giải chi tiết

1) a) Bán kính của hình cầu là: \(R = \dfrac{d}{2} = \dfrac{{50}}{2} = 25{\kern 1pt} {\kern 1pt} \left( {cm} \right)\)

Thể tích phần gạo hình cầu là: \({V_c} = \dfrac{1}{2} \cdot \dfrac{4}{3}\pi {R^3} = \dfrac{1}{2} \cdot \dfrac{4}{3}\pi {25^3} = \dfrac{{31{\kern 1pt} 250}}{3}\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)

Thể tích phần gạo vun lên dạng hình nón là: \({V_n} = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi \cdot {25^2} \cdot 12 = 2500\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)

Thể tích gạo trong thùng là: \({V_g} = \dfrac{{31{\kern 1pt} 250}}{3}\pi + 2500\pi = \dfrac{{38750}}{3}\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)

b) Thể tích lon là: \(\pi {.5^2}.14 = 350{\kern 1pt} \pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)

Thể tích gạo một ngày múc là: \(4.90\% .350\pi = 1260\pi {\kern 1pt} {\kern 1pt} \left( {c{m^3}} \right)\)

Ta có : \(\dfrac{{38{\kern 1pt} 750}}{\pi }:1{\kern 1pt} 260\pi \approx 10,3\)

Vậy cần ít nhất 11 ngày để dùng hết số gạo trong thùng.

a) Chứng minh bốn \(C,\,E,\,\,M,\,O\)cùng thuộc một đường tròn.

\(\Delta OBC\) cân tại \(O\), \(M\) là trung điểm của \(BC\) nên \(OM\)vừa là đường trung tuyến vừa là đường cao. Suy ra \(OM \bot BC \Rightarrow \angle {OMC} = 90^\circ \)

Theo bài ra, E là hình chiếu của C trên AK nên \(CE \bot AK \Rightarrow CE \bot EO \Rightarrow \angle {OEC} = {90^ \circ }\).

Gọi \(I\) là trung điểm của \(OC\)

Dễ dàng chứng minh \(IO = IE = IM = IC\)

Do đó C,E,M,O cùng thuộc một đường tròn \(\left( I \right)\).

b) *Chứng minh \(AD.AK = AB.AC\)

Xét \(\Delta DBA\) và \(\Delta CK{\rm{A}}\) có

+) \(\angle {ADB} = \angle {ACK} = 90^\circ \)

+) \(\angle {ABD} = \angle {AKC}\) (Hai góc nội tiếp cùng chắn cung AC)

Nên \(\Delta DBA\)~\(\Delta CK{\rm{A}}\)

Do đó ta có: \(\dfrac{{AD}}{{AB}} = \dfrac{{AC}}{{AK}}\) (cặp cạnh tương ứng tỉ lệ)

Hay \(AD.AK = AB.AC\) (đpcm).

*Chứng minh \(\Delta MDE\) cân.

Theo bài ra \(\left\{ \begin{array}{l}AD \bot BC\\AE \bot EC\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\angle {ADC} = 90^\circ \\\angle {AEC} = 90^\circ \end{array} \right.\)

Gọi \(Q\) là trung điểm của \(AC\)

Dễ dàng chứng minh \(QA = QC = QD = QE\)

Suy ra bốn điểm \(A,\,C,\,D,\,E\)cùng thuộc đường tròn \(\left( Q \right)\)

Suy ra \(\angle {CAE} = \angle {CDE}\) (Hai góc nội tiếp cùng chắn cung \(CE\))

Xét \(\left( O \right)\) ta có: \(\angle {CBK} = \angle {CAE}\) (Hai góc nội tiếp cùng chắn cung \(CK\))

Từ (1) và (2) suy ra \(\angle {CBK} = \angle {CDE}\) mà hai góc này ở vị trí đồng vị (3)

Suy ra DE // BK

Xét đường tròn \(\left( I \right)\)có: \(\angle {EMC} = \angle {EOC}\)(Hai góc nội tiếp cùng chắn cung EC). (4)

Xét đường tròn \(\left( O \right)\)có:\(\angle {KBC} = \dfrac{1}{2}\angle {KOC}\) (Góc nội tiếp và góc ở tâm cùng chắn cung KC). (5)

Từ (3); (4) và (5) suy ra: \(\angle {EMC} = 2\angle {CDE}\).

\(\Delta MDE\)có \(\angle {EMC} = \angle {MDE} + \angle {MED}\) (góc ngoài của tam giác) mà \(\angle {EMC} = 2\angle {MDE}\)

Nên \(\angle {MDE} = \angle {MED}\). Do đó, \(\Delta MDE\) cân tại \(M\).

c) Chứng minh khi \(A\) di chuyển trên cung lớn \(BC\) thì tâm đường tròn ngoại tiếp \(\Delta DEF\) là 1 điểm cố định.

Gọi \(P\) là trung điểm của \(BO\)

Dễ dàng chứng minh được \(PB = PO = PF = PM\)

Suy ra bốn điểm \(O,M,B,F\) cùng thuộc đường tròn \(\left( P \right)\)

Nên \(\angle {OBM} = \angle {MFO}\) (Hai góc nội tiếp cùng chắn cung MO).

Xét đường tròn \(\left( I \right)\)có: \(\angle {MEO} = \angle {MCO}\) \(CK\) (Hai góc nội tiếp cùng chắn cung MO).

Mà \(\angle {OBM} = \angle {OCM}\)(\(\Delta OCB\)cân tại \(O\)).

Do đó \(\angle {MFO} = \angle {MEO}\) \( \Rightarrow \Delta EMF\)cân tại \(M \Rightarrow ME = MF\)

Mà \(ME = MD\) (Tam giác \(MDE\)cân tại \(M\)).

Suy ra:\(MD = ME = ME\).

Suy ra \(M\) là tâm đường tròn ngoại tiếp tam giác \(DEF\).

Mà \(M\) là trung điểm của \(BC\)nên \(M\) là điểm cố định.

Vậy khi \(A\) di chuyển trên cung lớn \(BC\)thì tâm đường tròn ngoại tiếp tam giác \(DEF\)là một điểm cố định.

PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link