a) Trên bờ biển có hai trạm quan sát \(A\) và \(B\) cách nhau 10 km . Người

Câu hỏi số 769628:

Thông hiểu

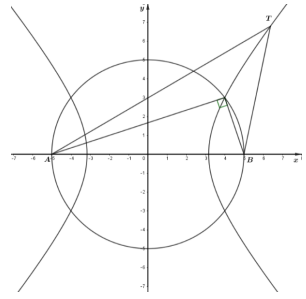
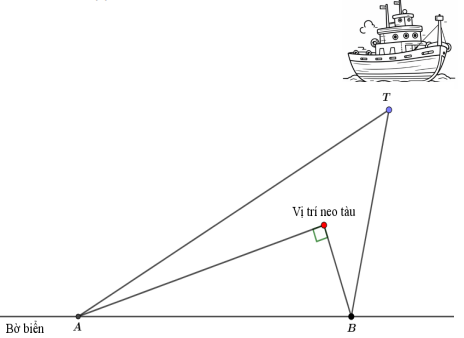
a) Trên bờ biển có hai trạm quan sát \(A\) và \(B\) cách nhau 10 km . Người ta điều khiển con tàu đang ở vị trí \(T\) đi vào bờ biển sao cho hiệu khoảng cách từ nó đến \(A\) và \(B\) luôn là \(2 \sqrt{10} \mathrm{~km}\) (tham khảo hình vẽ). Tính khoảng cách từ con tàu đến bờ biển khi tàu được neo lại và góc nhìn từ con tàu đến hai trạm quan sát là \(90^{\circ}\).

b) Đội văn nghệ của trường THPT Hòa Vang gồm 18 học sinh, trong đó có 7 học sinh khối lớp 12, 6 học sinh khối lớp 11 và 5 học sinh khối lớp 10. Tính số cách chọn 7 học sinh trong đội đi dự thi "Giai điệu tuổi hồng" sao cho mỗi khối có ít nhất một học sinh được chọn.

Quảng cáo

Xem lời giải

Câu hỏi:769628

Giải chi tiết

a) Chọn hệ trục toạ độ \(O x y\) như hình trên, trong đó 1 km ứng với 1 đơn vị.

Do \(\left\{\begin{array}{l}|T A-T B|=2 \sqrt{10} \\ A(-5 ; 0), B(5 ; 0)\end{array}\right.\) nên \(T\) thuộc hypebol \((H): \dfrac{x^2}{10}-\dfrac{y^2}{15}=1\).

Khi con tàu \(T\) được neo lại ta có \(\widehat{A T B}=90^{\circ}\)

Tức \(T\) thuộc đường tròn \((C): x^2+y^2=25\).

Lúc này tọa độ của \(T\) thoả mãn hệ:

\(\left\{\begin{array}{l}\dfrac{x^2}{10}-\dfrac{y^2}{15}=1 \\ x^2+y^2=25\end{array} \Leftrightarrow\left\{\begin{array}{l}x^2=16 \\ y^2=9\end{array} \Rightarrow|y|=3\right.\right.\)

Khi đó khoảng cách từ con tàu \(T\) đến bờ biển là 3km.

b) Ta có

Chọn 7 học sinh bất kỳ trong 18 học sinh là \(C_{18}^7=31824\) (cách)
Chọn 7 học sinh không đủ 3 khối
TH1: Chọn 7 học sinh thuộc cùng một khối (khối 12) có \(C_7^7=1\) cách.

TH2: Chọn 7 học sinh thuộc đúng hai khối
+ Chọn 7 học sinh thuộc hai khối 10 và 11 : có \(C_{11}^7=330\) cách.
+ Chọn 7 học sinh thuộc hai khối 10 và 12 : có \(C_{12}^7-C_7^7=791\) cách.
+ Chọn 7 học sinh thuộc hai khối 11 và 12 : có \(C_{13}^7-C_7^7=1715\) cách.
Vậy có: \(1+1+330+791+1715=2837\) cách.
Do đó, để chọn được 7 học sinh sao cho mỗi khối có ít nhất một em là:

\(31824-2837=28987\)

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10