Một quả cầu nhỏ khối lượng \({m_1} = 200g\) treo vào đầu một sợi dây nhẹ không

Câu hỏi số 774539:

Vận dụng

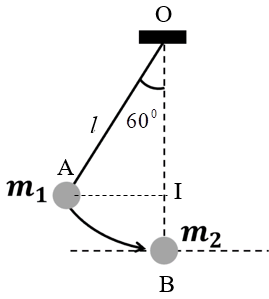
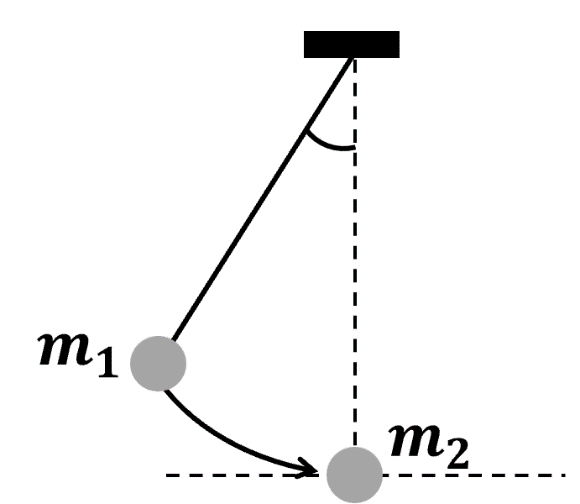
Một quả cầu nhỏ khối lượng \({m_1} = 200g\) treo vào đầu một sợi dây nhẹ không dãn có chiều dài l = 90 cm. Kéo quả cầu lệch khỏi vị trí cân bằng để dây treo hợp với phương thẳng đứng một góc \({60^0}\) rồi buông nhẹ. Bỏ qua ma sát và các lực cản. Cho \(g = 10\,\,m/{s^2}\). Tại vị trí cân bằng, quả cầu \({m_1}\) va chạm đàn hồi với quả cầu \({m_2} = 50g\) đang đứng yên trên mặt sàn nằm ngang. Tìm vận tốc của mỗi quả cầu ngay sau va chạm.

Quảng cáo

Xem lời giải

Câu hỏi:774539

Phương pháp giải

- Cơ năng: \(W = {W_d} + {W_t} = \dfrac{1}{2}m{v^2} + mgh\)

- Định luật bảo toàn cơ năng: Nếu vật chuyển động trong trọng trường chỉ chịu tác dụng bởi trọng lực thì cơ năng của nó được bảo toàn.

- Động lượng: \(\overrightarrow p = m.\overrightarrow v \)

- Định luật bảo toàn động lượng: “Động lượng toàn phần của hệ kín là một đại lượng bảo toàn”

\(\overrightarrow {{p_1}} + \overrightarrow {{p_2}} + ... + \overrightarrow {{p_n}} = \overrightarrow {{p_1}'} + \overrightarrow {{p_2}'} + ... + \overrightarrow {{p_n}'} \)

- Va chạm đàn hồi: Động năng của hệ sau va chạm bằng động năng của hệ trước va chạm.

Giải chi tiết

\(\begin{array}{l}{m_1} = 200g;l = 90cm;\alpha = {60^0}\\{m_2} = 50g;{v_2} = 0\end{array}\)

Gọi \({v_1}\) là tốc độ của quả cầu \({m_1}\) ngay trước khi va chạm với quả cầu \({m_2}\).

Chọn gốc thế năng tại B.

Cơ năng của quả cầu \({m_1}\) tại A là:

\(\begin{array}{l}{W_1} = {m_1}g.BI = {m_1}g.\left( {OB - OI} \right) = {m_1}g.\left( {l - l.\cos {{60}^0}} \right)\\ \Rightarrow {W_1} = {m_1}gl.\left( {1 - \cos {{60}^0}} \right)\end{array}\)

Cơ năng của quả cầu \({m_1}\) tại B là: \({W_2} = \dfrac{1}{2}{m_1}v_1^2\)

Áp dụng định luật bảo toàn cơ năng ta có:

\(\begin{array}{l}{W_2} = {W_1} \Leftrightarrow \dfrac{1}{2}{m_1}v_1^2 = {m_1}gl.\left( {1 - \cos {{60}^0}} \right)\\ \Rightarrow {v_1} = \sqrt {2gl.\left( {1 - \cos {{60}^0}} \right)} = \sqrt {2.10.0,9.\left( {1 - \dfrac{1}{2}} \right)} = 3m/s\end{array}\)

Động lượng của hệ hai quả cầu trước va chạm là: \(\overrightarrow {{p_{trc}}} = {m_1}.\overrightarrow {{v_1}} \)

Động lượng của hệ hai quả cầu sau va chạm là: \(\overrightarrow {{p_{sau}}} = {m_1}.\overrightarrow {{v_1}'} + {m_2}.\overrightarrow {{v_2}'} \)

Áp dụng định luật bảo toàn động lượng ta có:

\(\begin{array}{l}\overrightarrow {{p_{trc}}} = \overrightarrow {{p_{sau}}} \Leftrightarrow {m_1}.\overrightarrow {{v_1}} = {m_1}.\overrightarrow {{v_1}'} + {m_2}.\overrightarrow {{v_2}'} \\ \Rightarrow {m_1}.{v_1} = {m_1}.{v_1}' + {m_2}.{v_2}' \Leftrightarrow 200.3 = 200.{v_1}' + 50.{v_2}'\\ \Rightarrow 200.{v_1}' + 50.{v_2}' = 600 \Leftrightarrow 4{v_1}' + {v_2}' = 12\,\,\,\,\left( 1 \right)\end{array}\)

Va chạm của hai quả cầu là va chạm đàn hồi nên động năng của hệ sau va chạm bằng động năng của hệ trước va chạm:

\(\begin{array}{l}{W_{dsau}} = {W_{dtruoc}} \Leftrightarrow \dfrac{1}{2}{m_1}{v_1}{'^2} + \dfrac{1}{2}.{m_2}{v_2}{'^2} = \dfrac{1}{2}{m_1}v_1^2\\ \Leftrightarrow 200.{v_1}{'^2} + 50.{v_2}{'^2} = 200.9 \Leftrightarrow 5.{v_1}{'^2} + {v_2}{'^2} = 36\,\,\,\left( 2 \right)\end{array}\)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{ \begin{array}{l}4{v_1}' + {v_2}' = 12\\5.{v_1}{'^2} + {v_2}{'^2} = 36\end{array} \right. \Rightarrow \left[ \begin{array}{l}{v_1}' = \dfrac{{18}}{7}m/s;{v_2}' = \dfrac{{12}}{7}m/s\\{v_1}' = 2m/s;{v_2}' = 4m/s\end{array} \right.\)

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10