Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Thi thử toàn quốc cuối HK1 lớp 10, 11, 12 tất cả các môn - Trạm số 1 - Ngày 20-21/12/2025 Xem chi tiết
Giỏ hàng của tôi
Trang chủ
Luyện thi đại học môn toán

Trong không gian Oxyz (đơn vị trên mỗi trục tọa độ là killômét), một

Câu hỏi số 774772:
Vận dụng

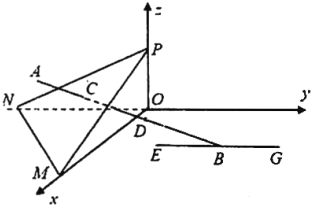
Trong không gian Oxyz (đơn vị trên mỗi trục tọa độ là killômét), một máy bay đang ở vị trí $A(4; - 0,5;0,5)$ và sẽ hạ cánh ở vị trí $B(3;2,5;0)$ ở trên đường băng EG (hình vẽ). Có một lớp mây được mô phỏng bởi mặt phẳng $(\alpha)$ đi qua ba điểm $M(8;0;0),$$N(0; - 8;0)$ và $P(0;0;0,8)$.

Đúng Sai
a) Đường thẳng AB có phương trình tham số là: $\left\{ \begin{array}{l} {x = 4 - t} \\ {y = - 0,5 + 3t} \\ {z = 0,5 - 0,5t} \end{array} \right.$$\left( {t \in {\mathbb{R}}} \right)$
b) Khi máy bay cách mặt đất 120 m thì vị trí của máy bay trên đường thẳng AB là điểm $D(3,24;1,78;0,12)$.
c) Độ cao của máy bay khi xuyên qua đám mây để hạ cánh là $0,42~\text{km}$ (làm tròn kết quả tớ hàng phà̀n trăm).
d) Theo quy định an toàn bay, người phi công phải nhìn thấy điểm cuối $G(4,5;5,5;0)$ của đường băng ở độ cao tối thiểu là 120m. Nếu sau khi ra khỏi đám mây tầm nhìn của người phi công là 900m thì người phi công đã đạt được quy định an toàn bay.

Đáp án đúng là: Đ; Đ; Đ; S

Quảng cáo

Xem lời giải
Câu hỏi:774772
Phương pháp giải

Tọa độ hóa, viết phương trình đường thẳng, tìm tọa độ điểm.

Giải chi tiết

a) Đúng: Ta có $\overset{\rightarrow}{AB} = \left( {- 1;3; - 0,5} \right)$

Đường thẳng AB đi qua điểm $A(4; - 0,5;0,5)$và nhận vectơ $\overset{\rightarrow}{AB} = \left( {- 1;3; - 0,5} \right)$ làm một vtcp.

Suy ra phương trình đường thẳng AB là: $\left\{ \begin{array}{l} {x = 4 - t} \\ {y = - 0,5 + 3t} \\ {z = 0,5 - 0,5t} \end{array} \right.$$\left( {t \in {\mathbb{R}}} \right)$.

b) Đúng: Máy bay cách mặt đất 120m = 0,12km nghĩa là $\left. z = 0,12 =0,5 - 0,5t\Rightarrow t = \dfrac{19}{25}. \right.$

Suy ra vị trị của máy bay khi cách mặt đất 120 m là:

$\left. \left\{ \begin{matrix} {x_{D} = 4 - \dfrac{19}{25} = 3,24} \\ {y_{D} = - 0,5 + 3.\dfrac{19}{25} = 1,78} \\ {z_{D} = 0,12} \end{matrix} \right.\Rightarrow D\left( {3,24;1,78;0,12} \right) \right.$

c) Đúng: Gọi $C$ là giao điểm của đường thẳng AB và mặt phẳng $\left( {MNP} \right)$.

Ta cần tìm tọa độ điểm $C.$

Phương trình $mp\left( {MNP} \right)$ là: $\left. \dfrac{x}{8} + \dfrac{y}{- 8} + \dfrac{z}{0,8} = 1\Rightarrow x - y + 10z - 8 = 0. \right.$

Vì $C = AB \cap mp\left( {MNP} \right)$

$\left. \Rightarrow 4 - t - \left( {- 0,5 + 3t} \right) + 10\left( {0,5 - 0,5t} \right) - 8 = 0\Rightarrow t = \dfrac{1}{6}. \right.$

Suy ra tọa độ điểm C là $C\left( {\dfrac{23}{6};0;\dfrac{5}{12}} \right)$

Vậy độ cao của máy bay khi xuyên qua đám mây để hạ cánh là $\dfrac{5}{12}\text{km} \approx \text{0,42km}\text{.}$

d) Sai: Khi máy bay cách mặt đất 120 m , nó đang ở vị trí điểm D. DG là tầm nhìn của phi công tới E khi cách mặt đất 120 m .

Ta có: $DG = \sqrt{{(4,5 - 3,24)}^{2} + {(5,5 - 1,78)}^{2} + {(0 - 0,12)}^{2}} \approx 3,93(~\text{km})$.

Vi tầm nhìn của phi công sau khi ra khỏi đám mây là $900~\text{m} = 0,9~\text{km} < 3,93~\text{km}$ nên người phi công đó không nhìn thấy G , do đó không đạt được quy định an toàn bay.

Đáp án cần chọn là: Đ; Đ; Đ; S

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn