Dựa vào thông tin dưới đây để trả lời các câu sauMột cửa hàng bán sữa có kế hoạch nhập
Dựa vào thông tin dưới đây để trả lời các câu sau
Một cửa hàng bán sữa có kế hoạch nhập về hai loại sữa $A$ và $B$ để bán với số vốn không vượt quá 20 triệu đồng. Giá 1 thùng sữa loại $A$ là 300 nghìn đồng và loại $B$ là 400 nghìn đồng. Nếu cửa hàng bán được 1 thùng sữa loại $A$ sẽ mang lại lợi nhuận 80 nghìn đồng và bán được 1 thùng sữa loại $B$ mang lại lợi nhuận 100 nghìn đồng. Cửa hàng ước tính rằng tổng nhu cầu khách mua hàng tháng sẽ không vượt quá 60 thùng.
Trả lời cho các câu 1, 2 dưới đây:
Nếu số thùng sữa mà cửa hàng cần nhập loại A là x (thùng) và loại B là y (thùng), số tiền để nhập hai loại sữa với số lượng như trên là
Đáp án đúng là: C
Dựa vào thông tin giá 1 thùng sữa loại $A$ là 300 nghìn đồng và loại $B$ là 400 nghìn đồng
Đáp án cần chọn là: C
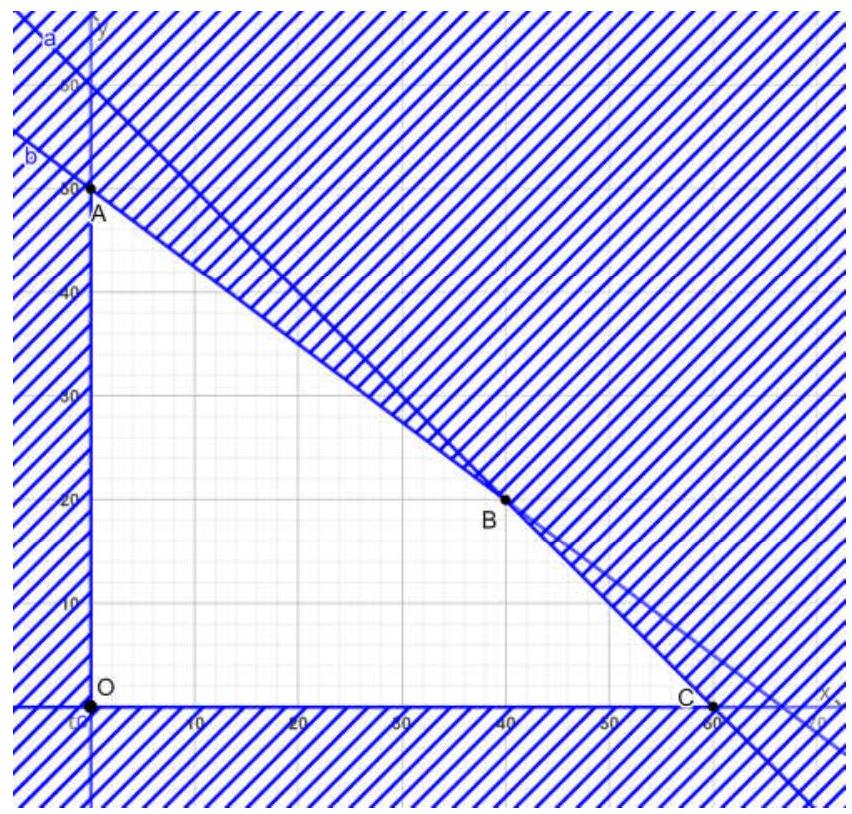
Tìm số lượng thùng sữa mỗi loại cửa hàng cần nhập về trong tháng đó để lợi nhuận thu được là lớn nhất.
Đáp án đúng là: A
Xét miền nghiệm, tìm điểm có giá trị lớn nhất
Giả sử số thùng sữa mà cửa hàng cần nhập loại A là x (thùng) và loại B là y (thùng) với $x \geq 0;y \geq 0$.
Vì nhu cầu của thị trường không vượt quá 60 thùng nên $x + y \leq 60$.
Số tiền để nhập hai loại sữa với số lượng như trên là: $300\text{x} + 400\text{y}$ (nghìn đồng).
Số tiền để nhập cho hai loại sữa này không vượt quá 20 triệu đồng, nên ta có
$300x + 400y \leq 20000$ hay $3x + 4y \leq 200$.
Từ đó ta thu được hệ bất phương trình bậc nhất hai ẩn sau: $\left\{ \begin{array}{l} {x \geq 0} \\ {y \geq 0} \\ {x + y \leq 60} \\ {3x + 4y \leq 200} \end{array} \right.$
Lợi nhuận thu được khi bán hết số sữa trên là $F\left( {x;y} \right) = 80x + 100y$ (nghìn đồng).
Ta cần tìm giá tri lớn nhất của $F\left( {x;y} \right)$ khi $\left( {x;y} \right)$ thoả mãn hệ bất phương trình trên.
Miền nghiệm của hệ bất phương trình trên là miền tứ giác $OABC$ với toạ độ các đỉnh $\text{O}\left( {0;0} \right),\text{A}(0$; $50),\text{B}\left( {40;20} \right)$ và $\text{C}\left( {60;0} \right)$. Ta tính được các giá trị tương ứng của $F\left( {x;y} \right) = 80x + 100y$ là: $0;5000$; 5200; 4800 (nghìn).
Vậy cửa hàng cần nhập 40 thùng sữa loại A và 20 thùng sữa loại B để lợi nhuận thu được là lớn nhất.
Đáp án cần chọn là: A
Quảng cáo
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
