1) Một xe bồn chở nước sạch cho một cụm dân cư có 100 hộ dân. Mỗi đầu của bồn chứa
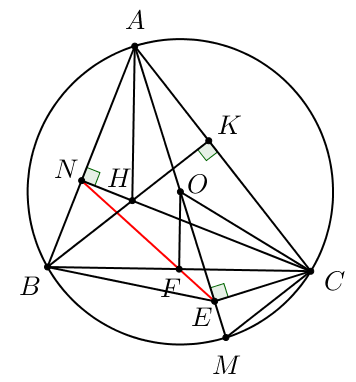
1) Một xe bồn chở nước sạch cho một cụm dân cư có 100 hộ dân. Mỗi đầu của bồn chứa nước là nừa hình cầu, thân bồn chứa nước là hình trụ (có kích thước như hình vẽ). Bồn chứa đầy nước và lượng nước được chia đều cho từng hộ dân. Hỏi mỗi hộ dân nhận được bao nhiêu mét khối nước sạch? (kết quả làm tròn đến chữ số thập phân thứ hai, lấy $\pi = 3,14$)
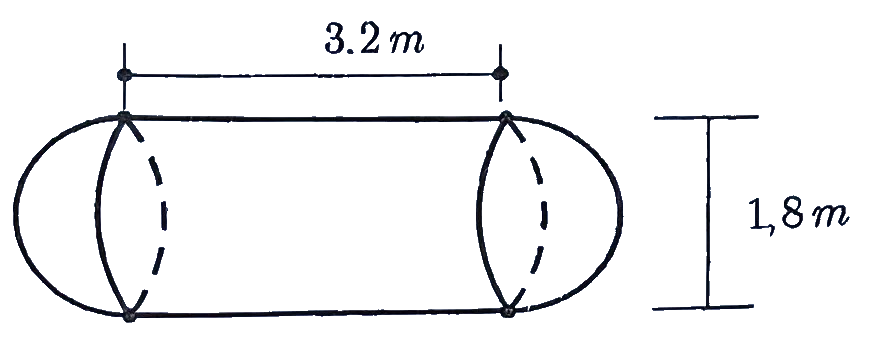
2) Cho tam giác ABC nhọn nội tiếp đường tròn tâm O (AB < AC). Vẽ các đường cao BK và CN cắt nhau tại H.
a) Chứng minh tứ giác BNKC nội tiếp.
b) Kẻ đường kính AM của đường tròn (O), kẻ CE vuông góc với AM (E thuộc AM). Chứng minh $\angle ABH = \angle NEA$.
c) Cho B, C là hai điểm cố định và điểm A di động trên cung lớn BC sao cho tam giác ABC nhọn và AB < AC. Chứng minh NE luôn đi qua một điểm cố định.
Quảng cáo
1) Thể tích của cả bồn chứa nước = Thể tích phần thân bồn chứa nước + Thể tích hai đầu của bồn chứa nước.
2) a) Chứng minh B, C, K, N cùng thuộc đường tròn đường kính BC hay tứ giác BNKC nội tiếp.
b) Chứng minh A, N, E, C cùng thuộc đường tròn đường kính AC
Khi đó $\angle NEA = \angle NCA$ (cùng chắn cung AN)
Mà $\angle NBK = \angle NCK$ (cùng chắn cung NK)
Suy ra $\angle NBK = \angle NEA$
c) Gọi F là trung điểm của BC
Chứng minh OFEC nội tiếp nên $\angle EFC = \angle EOC$ (cùng chắn EC) (1)
Chứng minh $\angle MOC = \angle NFB$ (2)
Từ (1) và (2) suy ra $\angle EFC = \angle NFB$
Mà $\angle NFB + \angle NFC = 180^{0}$ nên $\angle EFC + \angle NFE = 180^{0}$ hay N, F, E thẳng hàng
Do B, C cố định nên trung điểm F cố định. Chứng tỏ NE luôn đi qua điểm F cố định.
1) Phần thân bồn chứa nước là hình trụ có chiều cao bằng 3,2m và bán kính đáy bằng $1,8:2 = 0,9$m
Khi đó thể tích phần thân bồn chứa nước là $\pi.R^{2}h = 3,14.0,9^{2}.3,2 = 8,13888$ m3
Hai đầu của bồn chứa nước tạo thành một hình cầu có bán kính bằng 0,9m nên có thể tích là $\dfrac{4}{3}\pi.R^{3} = \dfrac{4}{3}.3,14.0,9^{3} = 3,05208$ m3 nước
Vậy thể tích của cả bồn chứa nước là $8,13888 + 3,05208 = 11,19096$ m3 nước
Vậy mỗi hộ dân nhận được $11,19096:100 \approx 0,11$ m3 nước.
2)
a) Do $BK\bot AC$ nên $\Delta BKC$ vuông tại K nên B, K, C cùng thuộc đường tròn đường kính BC
$CN\bot AB$ nên $\Delta BNC$ vuông tại N nên B, N, C cùng thuộc đường tròn đường kính BC
Vậy B, C, K, N cùng thuộc đường tròn đường kính BC hay tứ giác BNKC nội tiếp.
b) Ta có $\Delta AEC$ vuông tại E và $\Delta ANC$ vuông tại N nên A, N, E, C cùng thuộc đường tròn đường kính AC
Khi đó $\angle NEA = \angle NCA$ (cùng chắn cung AN)
Mà $\angle NBK = \angle NCK$ (cùng chắn cung NK)
Suy ra $\angle NBK = \angle NEA$ hay $\angle ABH = \angle NEA$
c) Gọi F là trung điểm của BC
Vì $\Delta OBC$ cân tại O có OF là trung tuyến nên đồng thời là đường cao
Suy ra $OF\bot BC$ hay $\Delta OFC$ vuông tại F nên O, F, C cùng thuộc đường tròn đường kính OC
Ta có $\Delta OEC$ vuông tại E nên O, E, C thuộc đường tròn đường kính OC
Vậy OFEC nội tiếp nên $\angle EFC = \angle EOC$ (cùng chắn EC) (1)
Vì $\Delta OMC$ cân tại O nên $\angle MOC = 180^{0} - 2\angle OMC$
Vì $\Delta FBN$ cân tại F nên $\angle NFB = 180^{0} - 2\angle FBN$
Mà $\angle OMC = \angle FBN$ (cùng chắn cung AC) nên $\angle MOC = \angle NFB$ (2)
Từ (1) và (2) suy ra $\angle EFC = \angle NFB$
Mà $\angle NFB + \angle NFC = 180^{0}$ nên $\angle EFC + \angle NFE = 180^{0}$ hay N, F, E thẳng hàng
Do B, C cố định nên trung điểm F cố định. Chứng tỏ NE luôn đi qua điểm F cố định.
PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
