a) Xét $x,y,z$ là các số thực dương thỏa mãn $xy + yz + zx \leq xyz$. Tìm giá trị nhỏ nhất của

Câu hỏi số 798336:

Vận dụng

a) Xét $x,y,z$ là các số thực dương thỏa mãn $xy + yz + zx \leq xyz$. Tìm giá trị nhỏ nhất của biểu thức $Q = xy^{2} + yz^{2} + zx^{2} - 18\left( {x + y + z} \right)$.
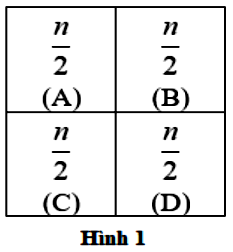
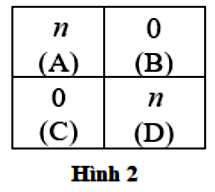
b) Cho bảng hình chữ nhật gồm 2 dòng và $n$ cột, được chia đều thành $2n$ ô vuông đơn vị. Ban đầu, trong mỗi ô vuông đơn vị người ta đặt đúng một viên bi có kích thước rất nhỏ. Ta gọi mỗi biến đổi $\left( \text{T} \right)$ là việc thực hiện các thao tác sau: Chọn ra hai ô vuông đơn vị tùy ý có chứa bi, chuyển từ mỗi ô vuông đó đi một viên bi sang ô vuông đơn vị liền kề (hai ô vuông đơn vị gọi là liền kề nếu chúng có chung cạnh). Tìm tất cả các số nguyên dương $n$ để sau hữu hạn lần chỉ thực hiện biến đổi $\left( \text{T} \right)$, ta có thể đưa hết tất cả các viên bi có trên bảng lúc đầu về nằm trong cùng một ô vuông đơn vị của bảng.

Quảng cáo

Xem lời giải

Câu hỏi:798336

Phương pháp giải

a) Từ giả thiết có $1 \geq \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}$. Dùng bất đẳng thức Cauchy-Schwarz có $xy^{2} + yz^{2} + zx^{2} \geq \left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)\left( {xy^{2} + yz^{2} + zx^{2}} \right) \geq {(y + z + x)}^{2}$.

b) Xét $n$ là số lẻ:
Ta tô màu các ô vuông đơn vị theo kiểu xen kẽ như bàn cờ vua bởi hai màu đen, trắng. Gọi $B,W$ lần lượt là số bi nằm ở ô đơn vị màu đen, số bi nằm ở ô đơn vị màu trắng.

Lúc đầu: $B = n$ và $W = n$. Như vậy $B,W$ là các số lẻ.

Giải chi tiết

Suy ra $Q \geq {(x + y + z)}^{2} - 18\left( {x + y + z} \right) = {(x + y + z - 9)}^{2} - 81 \geq - 81$.
Khi $x = y = z = 3$ thì các giả thiết được thỏa mãn và $Q = - 81$.

Vậy giá trị nhỏ nhất của $Q$ bằng -81.

Cách khác: $Q + 81 \geq xy^{2} - 18y + \dfrac{81}{x} + yz^{2} - 18z + \dfrac{81}{y} + zx^{2} - 18x + \dfrac{81}{z}$

$= x\left( {y - \dfrac{9}{x}} \right)^{2} + y\left( {z - \dfrac{9}{y}} \right)^{2} + z\left( {x - \dfrac{9}{z}} \right)^{2} \geq 0$

Lúc đầu: $B = n$ và $W = n$. Như vậy $B,W$ là các số lẻ.

Chỉ ra được bất biến: Sau mỗi lần thực biến đổi $\left( \text{T} \right)$ thì tính chẵn lẻ của $B,W$ là không thay đổi.

Suy ra lúc nào cũng có bi nằm ở ô đen và lúc nào cũng có bi nằm ở ô trắng (vì $B,W$ luôn là số lẻ), vậy không thể dồn hết tất cả các viên bi về một ô vuông đơn vị.

Xét $n$ là số chẵn: Ta chỉ ra cách dồn được bi theo yêu cầu.

Đầu tiên ta chọn hai ô vuông phân biệt mà mỗi ô vuông tương ứng đều nằm ở cuối cùng của mỗi dòng và phải có bi, thực hiện biến đổi $(T)$ để dồn hết bi từ hai ô này về hai ô đứng liền trước chúng. Lại thực hiện tiếp biến đổi $\left( \text{T} \right)$ với hai ô đơn vị có bi mà mỗi ô nằm ở đầu ngoài cùng của mỗi dòng để dồn hết bi của hai ô này về hai ô đứng liền sau chúng. Tiếp tục với hai cách chọn ô như vậy (chọn cặp ô có bi ở cuối dòng rồi lại chọn cặp ô có bi ở đầu dòng) ta đi đến trạng thái bi chỉ còn nằm ở bảng con $2 \times 2$ ở chính giữa của bảng ban đầu như hình 1 (các chữ cái ghi trong ngoặc là để chỉ tên của ô, các số chỉ số lượng bi đang có ở ô tương ứng đó).

Tiếp theo chọn cặp ô $\text{B},\text{C}$ và thực hiện $\dfrac{n}{2}$ lần biến đổi $\left( \text{T} \right)$ (bi từ ô B đưa sang ô $\text{A}$, bi từ ô C đưa sang ô $\text{D}$) thì thu được trạng thái như hình 2.

Tiếp tục, ta liên tục chọn cặp ô $\text{A},\text{D}$ cho đến khi hết bi và chuyển bi ở hai ô này sang ô C thì sau cùng đưa được $2n$ viên bi về hết ô C.

Vậy tập hợp tất cả các số $n$ cần tìm là tập các số nguyên dương chẵn.

PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link