Vật dao động điều hòa có vận tốc cực đại bằng 3 m/s và gia tốc cực đại bằng \(30\pi

Vật dao động điều hòa có vận tốc cực đại bằng 3 m/s và gia tốc cực đại bằng $30\pi \,\,m/{s^2}$. Thời điểm ban đầu vật có vận tốc 1,5 m/s và thế năng đang giảm.

Trả lời cho các câu 1, 2 dưới đây:

Câu hỏi số 1:

Vận dụng

Xác định li độ của vật ở thời điểm đầu. (Đơn vị: cm, làm tròn đến chữ số hàng phần mười).

Trả lời:

Đáp án đúng là:

Xem lời giải

Câu hỏi:818268

Phương pháp giải

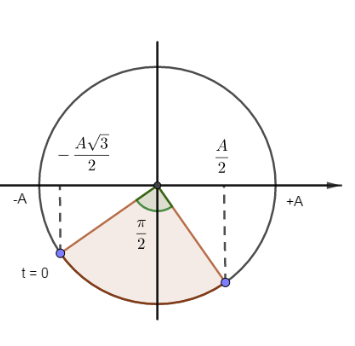
Áp dụng các công thức cực trị: ${v_{\max }} = \omega A;\,\,{a_{\max }} = {\omega ^2}A$ và công thức độc lập với thời gian: ${x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2};\,\,a = - {\omega ^2}x$.

Giải chi tiết

Ta có: $\left\{ \begin{array}{l}{v_{\max }} = \omega A = 300\,\,cm/s\\{a_{\max }} = {\omega ^2}A = 3000\pi \,\,cm/{s^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}A = \dfrac{{30}}{\pi }\,\,\left( {cm} \right)\\\omega = 10\pi \,\,\left( {rad/s} \right)\end{array} \right.$

Thời điểm ban đầu, vật có vận tốc 1,5 m/s = 150 cm/s, áp dụng công thức độc lập với thời gian, ta có:

${x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow {x^2} + \dfrac{{{{150}^2}}}{{{{\left( {10\pi } \right)}^2}}} = {\left( {\dfrac{{30}}{\pi }} \right)^2} \Rightarrow x = \pm \dfrac{{15\sqrt 3 }}{\pi }\left( {cm} \right) = \dfrac{{ \pm A\sqrt 3 }}{2}$

Thế năng đang giảm $ \Rightarrow x = \dfrac{{ - A\sqrt 3 }}{2}$ và chuyển động theo chiều dương.

Vậy li độ của vật ở thời điểm đầu là:

$x = - \dfrac{A\sqrt{3}}{2} = - \dfrac{15\sqrt{3}}{\pi} \approx - 8,3\,\,\left( {cm} \right)$

Đáp án cần điền là: -8,3

Câu hỏi số 2:

Vận dụng

Xác định thời điểm vật có gia tốc $ - 15\pi \,\,m/{s^2}$ lần đầu tiên. (Đơn vị: giây).

Trả lời:

Đáp án đúng là:

Xem lời giải

Câu hỏi:818269

Phương pháp giải

Sử dụng vòng tròn lượng giác và công thức $\Delta t = \dfrac{{\Delta \varphi }}{\omega }$.

Giải chi tiết

Thời điểm vật có gia tốc bằng $ - 15\pi \,\,m/{s^2}$, ta có:

$\begin{array}{l} a = - 15\pi {\mkern 1mu} \left( {m/{s^2}} \right) = - \dfrac{{30\pi }}{2} \Rightarrow a = - \dfrac{{{a_{\max }}}}{2}\\ \Rightarrow - {\omega ^2}x = - \dfrac{{{\omega ^2}A}}{2} \Rightarrow x = \dfrac{A}{2} \end{array}$

Ta có VTLG:

Từ VTLG, ta thấy vật chuyển động từ vị trí $x = \dfrac{{ - A\sqrt 3 }}{2}$ đến vị trí $x = \dfrac{A}{2}$, góc quét được là $\dfrac{\pi }{2}$

→ Thời điểm vật có gia tốc bằng $ - 15\pi \,\,m/{s^2}$: $t = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{\pi }{2}}}{{10\pi }} = 0,05\,\,\left( s \right)$

Đáp án cần điền là: 0,05

Quảng cáo

Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.