Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Giỏ hàng của tôi
Trang chủ
Toán 8

Đỉnh Fansipan (Lào Cai) cao 3143 m, là đỉnh núi cao nhất Đông Dương. Trên

Câu hỏi số 843025:
Vận dụng

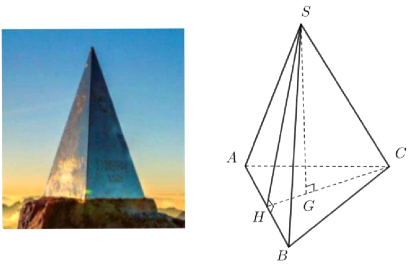
Đỉnh Fansipan (Lào Cai) cao 3143 m, là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi, người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều dài 60 cm, chiều cao 90 cm (như hình vẽ).

Đúng Sai
a) Tam giác đều ABC có CH là đường trung tuyến.
b) Độ dài cạnh CH bằng \(30 \sqrt{3} \mathrm{~cm}\).
c) Độ dài cạnh SH nhỏ hơn độ dài cạnh CH.
d) Diện tích xung quanh của hình chóp S.ABC là \(8635 \mathrm{~cm}^2\).

Đáp án đúng là: Đ; Đ; S; S

Quảng cáo

Xem lời giải
Câu hỏi:843025
Phương pháp giải

a, b) Áp dụng công thức đường cao tam giác đều để tính CH và GH$.
c) Sử dụng định lý Pythagore trong $\Delta SGH$ vuông tại G để tính trung đoạn SH và so sánh độ dài với CH.

d) Áp dụng công thức $S_{xq} = p \cdot d$ (với $p$ là nửa chu vi đáy, $d = SH$).

Giải chi tiết

a) Đúng: Mặt đáy của hình chóp \(S . A B C\) là một tam giác đều \(A B C\) có cạnh 60 cm. 

Gọi đường cao của mặt đáy là \(C H\) nên \(C H\) đồng thời là đường trung tuyến của tam giác đều \(A B C\). 

b) Đúng: Vì \(H A=H B=\dfrac{A B}{2}=30 \mathrm{~cm}\).
Áp dụng định lý Pythagore vào \(\triangle B H C\) vuông tại H , ta có:
\(C B^2=H B^2+H C^2\) hay \(60^2=30^2+H C^2 .\)
Suy ra \(C H^2=60^2-30^2=2700\) nên \(C H=\sqrt{2700}=30 \sqrt{3}(\mathrm{~cm})\). (1)
c) Sai: Gọi G là trọng tâm của mặt đáy nên \(G H=\dfrac{1}{3} H C=\dfrac{30 \sqrt{3}}{3}=10 \sqrt{3}(\mathrm{~cm})\).
Hình chóp \(S . A B C\) có đường cao \(S G\) nên \(S G \perp H C\).
Áp dụng định lý Pythagore với \(\triangle S H G\) vuông tại G , ta có:
\(S H^2=S G^2+H G^2=90^2+30^2=9000\)
Suy ra \(S H=\sqrt{9000}=30 \sqrt{10} \mathrm{~cm}\). (2)
Từ (1) và (2) suy ra độ dài cạnh \(S H\) lớn hơn độ dài cạnh \(C H\).

d) Sai: Nửa chu vi đáy là: \(P=\dfrac{1}{2}(60+60+60)=90(\mathrm{~cm})\)
Vậy diện tích xung quanh của hình chóp \(S . A B C\) là

\(S_{xq}=P \cdot d=90 \cdot 30 \sqrt{10} \approx 8538\left(\mathrm{~cm}^2\right)\).

Đáp án cần chọn là: Đ; Đ; S; S

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn