Một thùng hình hộp đáy phẳng chứa chất lỏng trong suốt có chiết suất $n = \sqrt{3}$. Chiều
Một thùng hình hộp đáy phẳng chứa chất lỏng trong suốt có chiết suất $n = \sqrt{3}$. Chiều cao của khối chất lỏng là $h = 4\, cm$. Đặt một nguồn sáng điểm S ở đáy thùng.
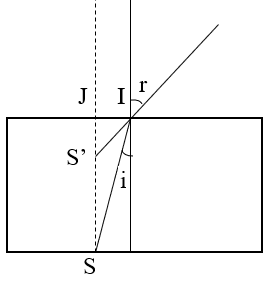
a) Từ ngoài không khí, một người quan sát nguồn sáng S theo phương vuông góc với mặt thoáng của khối chất lỏng thì thấy ảnh S' của S. Vẽ ảnh S' và dùng phương pháp hình học tính khoảng cách từ ảnh S' tới mặt chất lỏng.
b) Trong số các tia sáng phát ra từ S tới mặt thoáng của chất lỏng thì có những tia sáng khi tới mặt thoáng có tia khúc xạ và tia phản xạ vuông góc với nhau. Tìm góc tới của các tia sáng này.
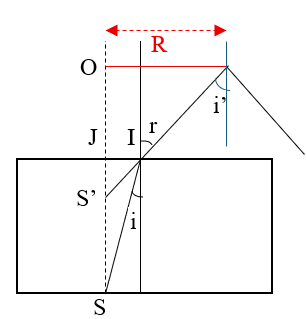
c) Đổ thêm một chất lỏng trong suốt khác có chiết suất n’=1,67 (nhẹ hơn và không trộn lẫn với chất lỏng ban đầu) vào thùng. Đặt trên mặt thoáng của chất lỏng này một tấm chắn sáng hình tròn bán kính $R = 5\ cm$, có tâm nằm trên đường thẳng đứng qua S. Tìm điều kiện của chiều cao lớp chất lỏng đổ thêm để không có tia sáng nào từ S chiếu ra ngoài không khí.
Quảng cáo
+ Áp dụng Định luật Khúc xạ ánh sáng: $n \cdot \sin i = 1 \cdot \sin r$.
+ Điều kiện vuông góc: Tia phản xạ và tia khúc xạ vuông góc với nhau: $\left. i + r = 90^{{^\circ}}\Rightarrow r = 90^{{^\circ}} - i \right.$.
+ Điều kiện không có tia sáng ra ngoài không khí: Tất cả các tia sáng phát ra từ S sau khi qua lớp chất lỏng thứ hai phải bị phản xạ toàn phần tại mặt thoáng trên cùng (giữa chất lỏng n' và không khí). Góc tới i' lớn nhất tại mặt phân cách trên cùng phải thỏa mãn điều kiện phản xạ toàn phần: $i' \geq i_{gh'}$, với $\sin i_{gh'} = \dfrac{1}{n'}$
a.
Vì quan sát theo phương vuông góc với mặt nước nên ta áp dụng được cho trường hợp góc nhỏ: $\sin i \approx \tan i;\sin r \approx \tan r$
Ta có: $\left. n.\sin i = \sin r\Rightarrow n.\tan i = \tan r \right.$
$\left. \Rightarrow\sqrt{3}.\dfrac{JI}{SJ} = \dfrac{JI}{S'J}\Rightarrow S'J = \dfrac{SJ}{\sqrt{3}} = \dfrac{4}{\sqrt{3}} \right.$cm
Suy ra khoảng cách từ ảnh S' tới mặt chất lỏng là $\dfrac{4}{\sqrt{3}}$ cm
b. Ta có: $\sqrt{3}.\sin i = \sin r;i + r = 90^{0}$
Giải hệ trên ta được: $i = 30^{0};r = 60^{0}$
Suy ra góc tới của tia sáng là 300
c. Hình vẽ:
Tại môi trường trên, điều kiện của I’ để không có tia sáng ra ngoài là:
$\left. \sin i_{gh}^{'} = \dfrac{1}{n'} = \dfrac{1}{1,67}\Rightarrow i' \geq i_{gh}^{'}\Rightarrow i' \geq 36,78^{0} \right.$
Từ đó: $r \geq 36,78^{0}$
Mà$\left. n\sin i = n'\sin r'\Rightarrow\sin i \geq \dfrac{1,67}{\sqrt{3}}.\sin 36,78^{0}\Rightarrow i \geq 35,26^{0} \right.$
$\left. \Rightarrow IJ = h.\tan i \geq 4.\tan 35,26^{0} = 2,828 \right.$
Mà $\left. \tan i' = \dfrac{IJ}{S'J}\Rightarrow S'J = \dfrac{IJ}{\tan i'} \geq \dfrac{2,828}{\tan 36,78^{0}} = 3,783 \right.$
Lại có: $\left. \tan i' = \dfrac{R}{h' + S'J}\Rightarrow\dfrac{5}{h' + 3,783} \geq 0,75\Rightarrow h' \leq 2,9 \right.$ cm
Vậy $h' \leq 2,9$ cm
PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
