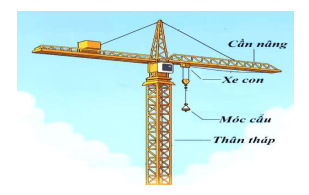
Người ta thường dùng cẩu trục tháp (như hình vẽ) để vận chuyển vật liệu

Câu hỏi số 846987:

Vận dụng

Người ta thường dùng cẩu trục tháp (như hình vẽ) để vận chuyển vật liệu xây dựng; thân tháp vuông góc với mặt đất, cần nâng vuông góc thân tháp dùng để làm điểm tựa nâng vật liệu, trên cần nâng có bộ phận gọi là xe con, có thể chạy dọc cần nâng nhằm di chuyển vật liệu. Ban đầu vật liệu ở mặt đất, cẩu trục dùng móc cẩu nâng vật liệu lên cao theo phương thẳng đứng và cao hơn $1m$ so với vị trí cần đặt, sau đó giữ nguyên độ cao và cẩu trục quay cần nâng một góc $\alpha \in (0{^\circ};180{^\circ})$ sao cho quỹ đạo tạo thành một cung tròn cho đến khi mặt phẳng $(P)$ chứa cần nâng và điểm cần đặt vuông góc với mặt đất (vật liệu và điểm cần đặt cùng nằm trên một nửa mặt phẳng $(P)$ so với thân tháp). Tiếp đến điều chỉnh xe con nhằm di chuyển và hạ vật liệu xuống $1m$ theo phương thẳng đứng đúng vị trí cần đặt. Giả sử rằng trục tọa độ $Oxyz$, thân tháp là trục $Oz$ và mặt đất là mặt phẳng $Oxy$ (đơn vị tính bằng mét); vị trí ban đầu của vật liệu là điểm $A(6;8;0)$ và vị trí cần đặt vật liệu là điểm $B(4; - 3;15)$. Tính quãng đường vật liệu đã di chuyển (kết quả làm tròn đến hàng phần chục).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:846987

Phương pháp giải

Xác định khoảng cách trong không gian.

Giải chi tiết

Gọi vị trí ban đầu là $A(6;8;0)$ và vị trí đích là $B(4; - 3;15)$. Tháp cẩu trùng với trục $Oz.$

+ Giai đoạn 1: Nâng vật liệu lên cao

Theo đề bài, vật liệu được nâng lên cao hơn vị trí đặt $1m$ tức là độ cao $h = 15 + 1 = 16m$

Vật đi từ độ cao $0m$ lên $16m.$

Quãng đường đi được là $S_{1} = 16m$

Vị trí mới của vật $A_{1}(6;8;16)$

+ Giai đoạn 2: Quay cần trục (Di chuyển theo cung tròn)

Bán kính quay là khoảng cách từ vật đến trục tháp $Oz.$$R = \sqrt{6^{2} + 8^{2}} = 10m$.

Cần trục quay vật liệu từ vị trí có phương vị của $A$ đến vị trí có phương vị của $B$

Xét vecto chỉ phương vị trong mặt phẳng $Oxy$$\overset{\rightarrow}{u} = \left( {6;8} \right)$ và $\overset{\rightarrow}{v} = \left( {4; - 3} \right)$

Gọi $\alpha$ là góc quay giữa hai vecto này, khi đó

$\left. \cos\alpha = \dfrac{\overset{\rightarrow}{u}.\overset{\rightarrow}{v}}{\left| \overset{\rightarrow}{u} \right|.\left| \overset{\rightarrow}{v} \right|} = \dfrac{6.4 + 8.\left( {- 3} \right)}{\sqrt{6^{2} + 8^{2}}.\sqrt{4^{2} + \left( {- 3} \right)^{2}}} = 0\Rightarrow\alpha = 90{^\circ} = \dfrac{\pi}{2}\left( {rad} \right) \right.$

Quãng đường di chuyển là $S_{2} = R.\alpha = 5\pi(m)$

+ Giai đoạn 3: Điều chỉnh xe con (Di chuyển theo phương bán kính)

Sau khi quay, vật liệu đang ở khoảng cách $R = 10m$ so với trục tháp.

Vị trí đích B có khoảng cách đến trục tháp là $r_{B} = \sqrt{4^{2} + \left( {- 3} \right)^{2}} = 5m$

Quãng đường đi được là $\left. S_{3} = \middle| 10 - 5 \middle| = 5m \right.$

+ Giai đoạn 4: Hạ vật liệu xuống

Vật liệu đang ở độ cao $16m$, đúng tọa độ ngang của B.

Hạ xuống vị trí cao $15m$ nên quãng đường $S_{4} = 1m$

Tổng quãng đường di chuyển là $S = 16 + 5\pi + 5 + 1 = 22 + 5\pi \approx 37,7m$

Đáp án cần điền là: 37,7

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.