Một bể chứa nước hình hộp chữ nhật $ABCDA'B'C'D'$ có chiều dài các cạnh

Câu hỏi số 848959:

Vận dụng

Một bể chứa nước hình hộp chữ nhật $ABCDA'B'C'D'$ có chiều dài các cạnh $AB = 4$ m, $AD = 3$ m và $AA' = 2\sqrt{3}$ m được đặt vào hệ trục tọa độ $Oxyz$ với đơn vị là mét như hình dưới. Trong bể đang chứa $12\sqrt{3}\mspace{6mu}(m^{3})$ nước và mặt nước chạm bốn cạnh $AA',BB',CC',DD'$ lần lượt tại $M,F,E,N$ . Một máy bơm, coi như một điểm $I \in (ME)$ được đặt trên mặt nước với vị trí của máy bơm thỏa mãn $\dfrac{MI}{ME} = \dfrac{2}{5}.$

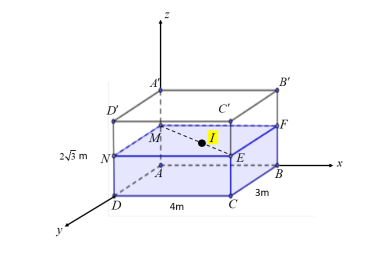
A diagram of a cube with lines and a black dot

AI-generated content may be incorrect.

Người ta nghiêng bể nước trên trục $Oy$ như hình vẽ dưới, khi đáy bể hợp với mặt phẳng $(Oxy)$ một góc $\alpha$ sao cho mặt nước lúc này chứa cạnh $A'D'$. Máy bơm lúc này vẫn nằm trên đoạn $ME$ ở vị trí thỏa mãn tỉ số $\dfrac{MI}{ME}$ như cũ.

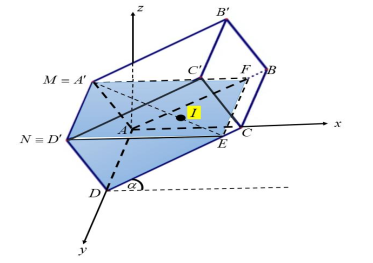
A diagram of a rectangle with lines and a yellow label

AI-generated content may be incorrect.

Lúc đó tọa độ của máy bơm là $I = (x_{0};y_{0};z_{0})$. Tính $\dfrac{x_{0}}{\sqrt{7}} + 5y_{0} + \dfrac{5z_{0}}{\sqrt{21}}$.

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:848959

Phương pháp giải

Xác định tỷ lệ nước trong bể sau đó xác định góc $\alpha$ và xác định tọa độ điểm mới theo $\alpha$

Giải chi tiết

Thể tích khối hộp là $V = 4.3.2\sqrt{3} = 24\sqrt{3}$, suy ra thể tích nước bằng một nửa thể tích khối hộp.

Suy ra sau khi nghiêng hộp thì điểm E sẽ trùng điểm C và điểm F sẽ trùng điểm B

Khi đó ta cần xác định tọa độ điểm M và E tức là A’ và C sau khi quay

Khi đó $\alpha$ bằng góc $\widehat{DCD^{\prime}}$ vì $\left( {ABCD} \right) \parallel \left( {Oxy} \right)$

Ta có $\left. D'C = \sqrt{4^{2} + \left( {2\sqrt{3}} \right)^{2}} = 2\sqrt{7}\Rightarrow\sin\alpha = \dfrac{\sqrt{3}}{\sqrt{7}},\cos\alpha = \dfrac{2}{\sqrt{7}} \right.$

Ta thấy nghiêng bể nước thì tung độ của điểm C không thay đổi, chỉ thay đổi hoành độ và cao độ.

Khi đó ta có hoành độ và cao độ mới của điểm C là $C_{x} = 4\cos\alpha$, $C_{z} = 4\sin\alpha$

Suy ra $C\left( {4\cos\alpha;3;4\sin\alpha} \right)$, tương tự $A'\left( {- 2\sqrt{3}\sin\alpha;0;2\sqrt{3}\cos\alpha} \right)$

Suy ra $C\left( {\dfrac{8}{\sqrt{7}};3;\dfrac{4\sqrt{3}}{\sqrt{7}}} \right)$ và $A'\left( {- \dfrac{6\sqrt{7}}{7};0;\dfrac{4\sqrt{21}}{7}} \right)$

Ta có $\left. \dfrac{IM}{IE} = \dfrac{2}{3}\Rightarrow 3\overset{\rightarrow}{IM} + 2\overset{\rightarrow}{IE} = 0\Rightarrow I = \dfrac{3M + 2E}{5} \right.$

$I = \dfrac{3A' + 2C}{5} = \left( {- \dfrac{2\sqrt{7}}{35};\dfrac{6}{5};\dfrac{4\sqrt{21}}{7}} \right)$

Vậy ta cần tính $\dfrac{x_{I}}{\sqrt{7}} + 5y_{I} + \dfrac{5z_{I}}{\sqrt{21}} = - \dfrac{2}{35} + 6 + \dfrac{20}{7} = 8,8$.

Đáp án cần điền là: 8,8

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.