Mái nhà tranh của ông $F$ được đặt vào trong hệ trục tọa độ $Oxyz$ với

Câu hỏi số 848962:

Vận dụng

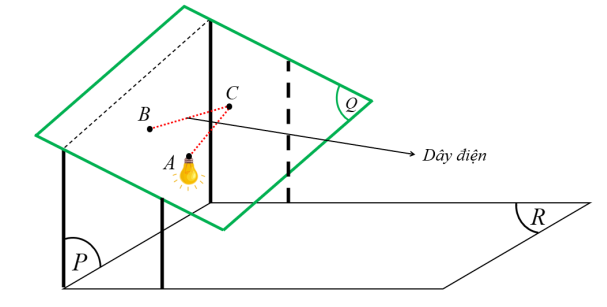
Mái nhà tranh của ông $F$ được đặt vào trong hệ trục tọa độ $Oxyz$ với đơn vị là mét với mặt phẳng $(R):z + 1 = 0$ là mặt đất. Một bức tường là mặt phẳng $(P):x + y - 2\sqrt{2} = 0$ và mái nhà lợp tranh của ông là mặt phẳng $(Q):x - z + \sqrt{2} = 0$. Ông $F$ muốn đặt một bóng đèn tròn để chiếu sáng ban đêm, sau khi cố định bóng đèn tại vị trí $A(1; - 1;1)$, ông nối dây điện thẳng dài từ bóng đèn đến vị trí một khoen móc đặt tại $C$ trên mái nhà $(Q)$ rồi luồn dây điện thẳng đến ổ cắm tại vị trí $B$ nằm trên bức tường $(P)$. Sau khi hoàn thành và đo đạc thì ông $F$ thấy tam giác $ABC$ là tam giác đều. Tính chiều cao mét của khoen móc $C$ so với mặt đất. (Làm tròn đến hàng phần chục).

A diagram of a triangle with a light bulb and lines

AI-generated content may be incorrect.

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:848962

Phương pháp giải

Để tính chiều cao của khoen móc $C$ so với mặt đất, ta xác định tọa độ của điểm $C$ dựa trên các điều kiện về mặt phẳng và tính chất của tam giác đều ABC.
Chiều cao của điểm $C\left(x_C, y_C, z_C\right)$ so với mặt đất là $h=z_C-(-1)=z_C+1$.

Giải chi tiết

Bức tường $(P):x + y - 2\sqrt 2 = 0$.

Mái nhà $(Q):x - z + \sqrt 2 = 0$.

Bóng đèn $A(1; - 1;1)$.

Có $d\left( {A,\left( P \right)} \right) = \dfrac{{|1 - 1 - 2\sqrt 2 |}}{{\sqrt {{1^2} + {1^2}} }} = \dfrac{{2\sqrt 2 }}{{\sqrt 2 }} = 2$,

$d\left( {A,\left( Q \right)} \right) = \dfrac{{|1 - 1 + \sqrt 2 |}}{{\sqrt {{1^2} + {{( - 1)}^2}} }} = \dfrac{{\sqrt 2 }}{{\sqrt 2 }} = 1$

Góc $\alpha$ giữa hai mặt phẳng $(P)$ và $(Q)$: $\cos \alpha = \dfrac{{|{{\vec n}_P} \cdot {{\vec n}_Q}|}}{{|{{\vec n}_P}| \cdot |{{\vec n}_Q}|}} = \dfrac{1}{2} \Rightarrow \alpha = {60^\circ }$

Vì $B \in (P)$ nên $AB \ge d(A,P) = 2$. Vì $C \in (Q)$ nên $AC \ge d(A,Q) = 1$.

Tam giác ABC đều nên $AB = AC = BC = a$. Từ $AB \ge 2$ suy ra $a \ge 2$.

Xét trường hợp cạnh $a$ nhỏ nhất tức là $a = 2$.

Khi $a = 2$, B là hình chiếu vuông góc của $A$ trên mặt phẳng $(P)$.

Đường thẳng qua A vuông góc với $(P)$: $\left\{ \begin{array}{l}x = 1 + t\\y = - 1 + t\\z = 1\end{array} \right.$

Thay vào $(P) \Rightarrow (1 + t) + ( - 1 + t) - 2\sqrt 2 = 0 \Rightarrow t = \sqrt 2 $.

Vậy $B(1 + \sqrt 2 ;\sqrt 2 - 1;1)$.

Điểm $C(x,y,z) \in (Q) \Rightarrow z = x + \sqrt 2 $, C thoả mãn $AC = 2$, $BC = 2$:

$A{C^2} = {(x - 1)^2} + {(y + 1)^2} + {(x + \sqrt 2 - 1)^2} = 4$

$B{C^2} = {(x - 1 - 2\sqrt 2 )^2} + {(y + 1 - \sqrt 2 )^2} + {(x + \sqrt 2 - 1)^2} = 4$

Suy ra $x + y = \sqrt 2 $, thay vào phương trình $A{C^2}$, ta được:

$A{C^2} = {(x - 1)^2} + {(\sqrt 2 - x + 1)^2} + {(x + \sqrt 2 - 1)^2} = 4$.

Suy ra $x = 1 \Rightarrow z = x + \sqrt 2 = 1 + \sqrt 2 $.

Chiều cao của khoen móc C so với mặt đất ($z = - 1$):

$h = \left( {1 + \sqrt 2 } \right) + 1 = 2 + \sqrt 2 \approx 3,4$.

Chú ý khi giải

Bài toán tồn tại vô số điểm C thoả mãn tam giác ABC đều. Tuy nhiên ở bài toán thực tế này, để giải ra được đáp án, ta chọn độ dài các cạnh $AB = AC = BC = 2$.

Đáp án cần điền là: 3,4

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.