Trong mùa mưa lũ, nước ở trên thượng nguồn đổ dồn về hạ lưu rất mạnh nên

Câu hỏi số 849484:

Vận dụng

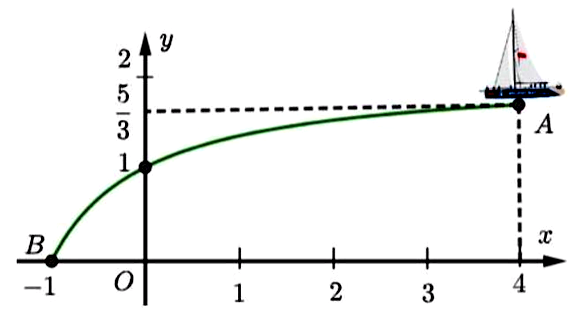
Trong mùa mưa lũ, nước ở trên thượng nguồn đổ dồn về hạ lưu rất mạnh nên thường làm lệch quỹ đạo chuyển động của tàu, thuyền trên sông. Giả sử trong một hệ trục tọa độ $Oxy$ cho trước, một chiếc thuyền đang ở tại điểm $A\left( {4;\dfrac{5}{3}} \right)$ và chuyển động về phía gốc tọa độ $O$. Do dòng chảy mạnh nên thuyền di chuyển trên cung đường $AB$ là một phần của đồ thị hàm số $y = \dfrac{ax + b}{cx + d}$ như hình vẽ, với $B\left( {- 1;0} \right)$. Gọi $M$ là một điểm bất kỳ nằm trên cung đường di chuyển của chiếc thuyền. Khoảng cách từ $M$ đến $O$ ngắn nhất bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:849484

Phương pháp giải

Từ $y = \dfrac{ax + b}{cx + d}$ qua $B\left( {- 1;0} \right)$ và $\left( {0;1} \right);\left( {4;\dfrac{5}{3}} \right)$ xác định hàm số

Gọi M theo tham số thuộc đồ thị và tìm tham số để OM nhỏ nhất với hoành độ M thuộc $\left( {- 1;0} \right)$

Giải chi tiết

Xét đường di chuyển A đến B là đồ thị $y = \dfrac{ax + b}{cx + d}$ với $- 1 \leq x \leq 4$

Do $y = \dfrac{ax + b}{cx + d}$ qua $B\left( {- 1;0} \right)$ và $\left( {0;1} \right);\left( {4;\dfrac{5}{3}} \right)$ nên ta có hệ

$\left\{ \begin{array}{l} {a.\left( {- 1} \right) + b = 0} \\ {\dfrac{b}{d} = 1} \\ {\dfrac{4a + b}{4c + d} = \dfrac{5}{3}} \end{array} \right.\Leftrightarrow\left\{ \begin{array}{l} {a = b} \\ {b = d} \\ {12a + 3b = 20c + 5d} \end{array} \right.$

$\Leftrightarrow\left\{ \begin{array}{l} {a = b = d} \\ {12a + 3a = 20c + 5a} \end{array} \right.\Leftrightarrow\left\{ \begin{array}{l} {a = b = d} \\ {c = \dfrac{a}{2}} \end{array} \right.$

Vậy $y = \dfrac{ax + b}{cx + d} = \dfrac{ax + a}{\dfrac{a}{2}x + a} = \dfrac{2x + 2}{x + 2} = 2 - \dfrac{2}{x + 2}$

Gọi điểm bất kì trên đồ thị là $M\left( {a - 2;2 - \dfrac{2}{a}} \right)$

Để khoảng cách từ M đến P ngắn nhất thì $OM = \sqrt{\left( {a - 2} \right)^{2} + \left( {2 - \dfrac{2}{a}} \right)^{2}}$ nhỏ nhất

Khi đó hoành độ M thuộc $\left( {- 1;0} \right)$ hay $\left. - 1 < a - 2 < 0\Leftrightarrow 1 < a < 2 \right.$

Ta có

$\begin{array}{l} {OM = \sqrt{\left( {a - 2} \right)^{2} + \left( {2 - \dfrac{2}{a}} \right)^{2}} = \sqrt{a^{2} - 4a + 4 + 4 - \dfrac{8}{a} + \dfrac{4}{a^{2}}}} \\ {= \sqrt{a^{2} + \dfrac{4}{a^{2}} - 4a - \dfrac{8}{a} + 8} = \sqrt{\left( {a + \dfrac{2}{a}} \right)^{2} - 4\left( {a + \dfrac{2}{a}} \right) + 4}} \\ {= \sqrt{\left( {a + \dfrac{2}{a} - 2} \right)^{2}} = \left| {a + \dfrac{2}{a} - 2} \right|} \end{array}$

Vì $a + \dfrac{2}{a} - 2 \geq 2\sqrt{a.\dfrac{2}{a}} - 2 = 2\sqrt{2} - 2$ nên $OM_{\min} = 2\sqrt{2} - 2 = 0,83$

Dấu = có khi $\left. a = \dfrac{2}{a}\Leftrightarrow a = \sqrt{2} \right.$ (thoả mãn)

Đáp án cần điền là: 0,83

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.