Một ngôi nhà hình lăng trụ đứng $ABCD \cdot A'B'C'D'$ có đáy $ABCD$

Câu hỏi số 849483:

Vận dụng

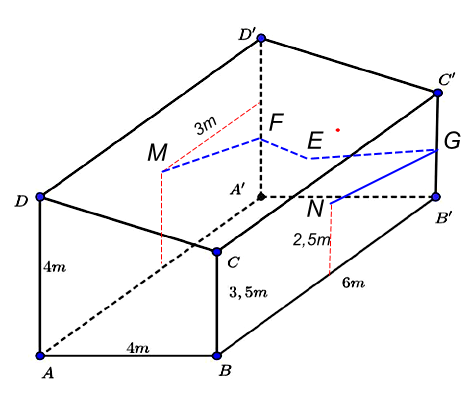
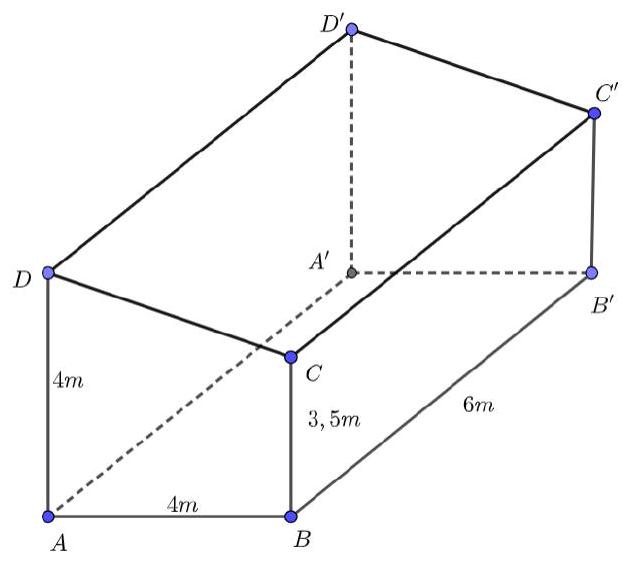
Một ngôi nhà hình lăng trụ đứng $ABCD \cdot A'B'C'D'$ có đáy $ABCD$ là hình thang vuông tại $A$ và $B$. $AB = AD = 4(m);BC = 3,5(m);BB' = 6m\ $ (xem hình vẽ). Ở bức tường $ADD'A'$ người ta lắp một bóng điện cách cạnh $A'D'$ một khoảng bằng $3(m)$ và cách mặt sàn một khoảng bằng $3(m)$, còn ở bức tường $BCC'B'$ người ta lắp một bóng điện cách cạnh $B'C'$ một khoảng bằng $3(m)$ và cách mặt sàn một khoảng bằng $2,5(m)$. Một bảng điều khiển được đặt tại bức tường $A'B'C'D'$ cách cạnh $A'D'$ một khoảng bằng $1(m)$ và cao $1,5(m)$ so với mặt sàn. Người ta muốn nối dây điện từ bảng điểu khiển men theo các bức tường (không mắc lên mái) đến 2 bóng điện trên. Hỏi cần tối thiểu bao nhiêu mét dây điện? (làm tròn kết quả đến hàng phần mười).

Trả lời:

Đáp án đúng là:

Quảng cáo

Xem lời giải

Câu hỏi:849483

Phương pháp giải

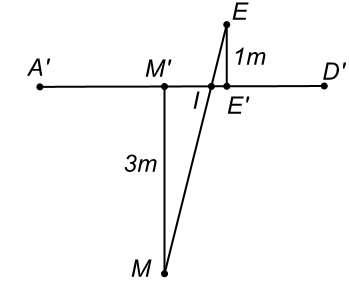
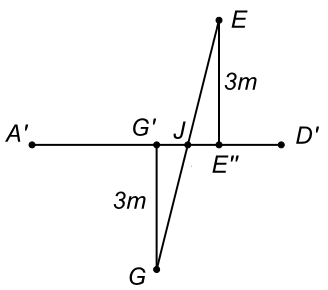
Dùng phương pháp trải phẳng để tính tổng khoảng cách ngắn nhất kết hợp với tỉ số Thales tính độ dài

Giải chi tiết

Khi đó gọi M là bóng đèn ở bức tường $ADD'A'$

N là bóng đèn ở bức tường $BCC'B'$

E là công tắc ở bức tường $A'B'C'D'$

Gọi F là điểm thuộc A’D’ nối E và M, gọi G là điểm thuộc B’C’ nối E và N

Khi đó đường dây điện là $NG + GE + EF + FM$

Do M, E, N cố định nên tổng đường dây nối ngắn nhất khi $\left( {MF + EF} \right)_{\min}$ và $\left( {EG + GN} \right)_{\min}$

Trải phẳng hai mặt $ADD'A'$ và $A'B'C'D'$ thành góc 180⁰ ta được

EE’ là khoảng cách từ E đến A’D’ nên EE’ = 1

MM’ là khoảng cách từ M đến A’D’ nên MM’ = 3

Vì E cách mặt sàn 1,5 m và M cắt mặt sàn 3m nên khoảng chênh lệch độ cao là M’E’ = 1,5m

Khi đó $\left. \dfrac{EE'}{MM'} = \dfrac{EI}{IM} = \dfrac{E'I}{M'I} = \dfrac{1}{3}\Rightarrow E'I = \dfrac{1}{3}M'I\Rightarrow E'I = \dfrac{1}{4}M'E' = \dfrac{1}{4}.1,5 = 0,375 \right.$

$\left. \Rightarrow MF + EF \geq EM = 4EI = 4\sqrt{1^{2} + 0,375^{2}} = \dfrac{\sqrt{73}}{2} \right.$ mét

Tương tự trải phẳng $BCC'B'$ và $A'B'C'D'$ thành góc 180⁰ ta được EE’’=3; GG;=3; G’E’’= 2,5 – 1,5 = 1

$\left. \Rightarrow\dfrac{EE^{''}}{GG'} = \dfrac{E^{''}J}{JG} = \dfrac{EJ}{GJ} = 1\Rightarrow G'J = 0,5 \right.$

$\left. \Rightarrow NG + GE \geq GE = 2GJ = 2\sqrt{3^{2} + 0,5^{2}} = \sqrt{37} \right.$

Vậy tổng đường dây nối nhỏ nhất bằng $\dfrac{\sqrt{73}}{2} + \sqrt{37} \approx 10,4$

Đáp án cần điền là: 10,4

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.