Tel: 024.7300.7989 - Phone: 1800.6947 (Thời gian hỗ trợ từ 7h đến 22h)

Giỏ hàng của tôi
Trang chủ
Luyện thi đại học môn toán

Dựa vào dữ liệu dưới đây, thí sinh lựa chọn một phương án đúng theo yêu cầu của câu 26

Dựa vào dữ liệu dưới đây, thí sinh lựa chọn một phương án đúng theo yêu cầu của câu 26 và câu 28.

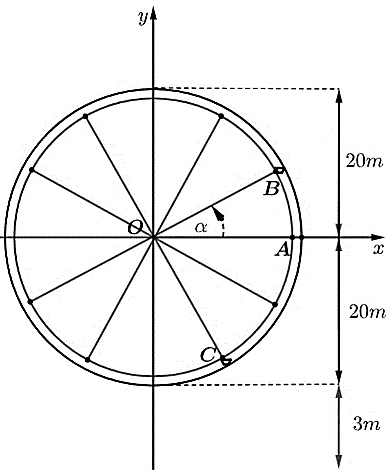
Một mô hình trò chơi vòng quay ở công viên có chiều cao tối đa 43 m so với mặt đất, bán kính vòng quay là 20 m. Hai bạn Hoa và Mai cùng chơi chung lượt quay và ngồi trong hai ca bin B, C mà góc $\widehat{BOC} = 90^{\circ}$ (tham khảo hình vẽ bên). Gọi $\alpha$ là góc lượng giác có tia đầu OA, tia cuối OB.

Trả lời cho các câu 1, 2, 3 dưới đây:

Câu hỏi số 1:
Thông hiểu

Khi $\alpha = 45^{\text{o}}$ thì chiều cao của B so với mặt đất (làm tròn kết quả đến hàng phần trăm) là

Đáp án đúng là: D

Xem lời giải
Câu hỏi:852196
Phương pháp giải

Tính chiều cao của $O$ so với mặt đất

Tính khoảng cách $B$ tới $OA$

Giải chi tiết

Khoảng cách từ $O$ tới mặt đất là $20 + 3 = 23(m)$

Khoảng cách từ $B$ tới $OA$ là $20\sin 45{^\circ} \approx 14,14\,\,(m)$

Do đó chiều cao của $B$ so với mặt đất là $23 + 14,14 = 37,14(m)$

Đáp án cần chọn là: D

Câu hỏi số 2:
Vận dụng

Khi Hoa ở vị trí có độ cao 33m so với mặt đất thì Mai ở độ cao bao nhiêu mét so với mặt đất (làm tròn kết quả đến hàng phần trăm)? Biết độ cao của Mai lúc này so với mặt đất là trên 10m

Đáp án đúng là: B

Xem lời giải
Câu hỏi:852197
Phương pháp giải

Giải phương trình $23 + 20\sin\alpha = 33$

Giải chi tiết

Khoảng cách từ $B$ đến $OA$ là $20\sin\alpha$

Theo bài ra ta có

$\begin{array}{l} {23 + 20\sin\alpha = 33} \\ \left. \Rightarrow\sin\alpha = 0,5 \right. \\ \left. \Rightarrow\left\lbrack \begin{array}{l} {\alpha = 30{^\circ}} \\ {\alpha = 150{^\circ}} \end{array} \right. \right. \end{array}$

Với $\left. \alpha = 30{^\circ}\Rightarrow\angle AOC = - 60{^\circ} \right.$

Khi đó độ cao của $C$ so với mặt đất là $23 + 20\sin\left( {- 60{^\circ}} \right) \approx 5,7 < 10$

Với $\left. \alpha = 150{^\circ}\Rightarrow\angle AOC = 60{^\circ} \right.$

Khi đó độ cao của $C$ so với mặt đất là $23 + 20\sin\left( {60{^\circ}} \right) \approx 40,32(m)$

Đáp án cần chọn là: B

Câu hỏi số 3:
Vận dụng

Chênh lệch độ cao của Mai và Hoa lớn nhất bằng bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?

Đáp án đúng là: D

Xem lời giải
Câu hỏi:852198
Phương pháp giải

Tính độ cao của Hoa, Mai so với mặt đất

Giải chi tiết

Độ cao của Hoa so với mặt đất là $h_{B} = 23 + 20\sin\alpha$

Độ cao của Mai so với mặt đất là $h_{C} = 23 + 20\sin\left( {\alpha - 90{^\circ}} \right)$

Khi đó $\left| {h_{B} - h_{C}} \right| = \left| {20\left( {\sin\alpha - \cos\alpha} \right)} \right| = 20\left| {\sqrt{2}\sin\left( {\alpha - \dfrac{\pi}{4}} \right)} \right|$

Ta có: $\sin\left( {\alpha - \dfrac{\pi}{4}} \right) \leq 1$ nên $20\left| {\sqrt{2}\sin\left( {\alpha - \dfrac{\pi}{4}} \right)} \right| \leq 20\sqrt{2}$

Đáp án cần chọn là: D

Quảng cáo

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>>  2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.

Hỗ trợ - Hướng dẫn

  • 024.7300.7989
  • 1800.6947 free

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com

Đăng ký nhận tư vấn