1) Cho phương trình $x^{2} + 7x - 5 = 0$ có hai nghiệm $x_{1},x_{2}$. Không giải phương

Câu hỏi số 855691:

Vận dụng

1) Cho phương trình $x^{2} + 7x - 5 = 0$ có hai nghiệm $x_{1},x_{2}$. Không giải phương trình hãy tính giá trị biểu thức: $P = \dfrac{x_{1}^{2} + x_{2}^{2}}{\left( {x_{1}^{2} + 7x_{1} - 6} \right)^{2025}}$.

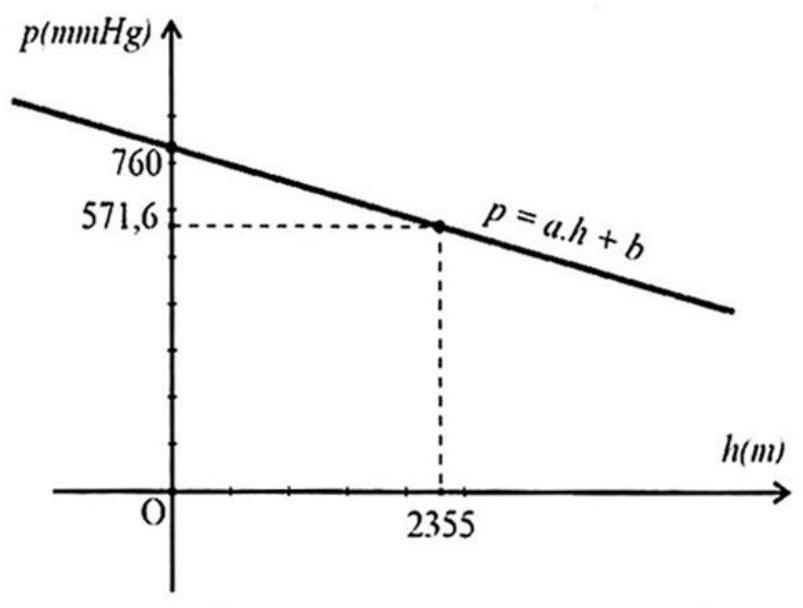
2) Càng lên cao không khí càng loãng nên áp suất khí quyển càng giảm. Người ta thấy với độ cao dưới 5000m thì mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất $p = a.h + b\left( {a \neq 0} \right)$ có đồ thị như hình vẽ bên. Trong đó: $p$ là đại lượng biểu thị cho áp suất của khí quyển (mmHg), $h$ là độ cao so với mặt nước biển (m) tại điểm đo áp suất. Những khu vực có độ cao ngang với mặt nước biển ($h = 0$) thì áp suất khí quyển là $p = 760$; thành phố A có độ cao $h = 2355$ thì $p = 571,6$. Một vận động viên leo núi, tại điểm dừng chân đo được áp suất khí quyển là 540 mmHg . Hãy tính độ cao của điểm dừng chân (so với mực nước biển).

Quảng cáo

Xem lời giải

Câu hỏi:855691

Phương pháp giải

1) Sử dụng hệ thức Vi-ét và biến đổi biểu thức về dạng tổng và tích các nghiệm. Chú ý tính chất nghiệm của phương trình ($Ax_{0}^{2} + Bx_{0} + C = 0$).

2) Xác định hàm số bậc nhất $p = ah + b$ dựa vào đồ thị hoặc các điểm đi qua. Giải phương trình bậc nhất để tìm ẩn.

Giải chi tiết

1) Phương trình $x^{2} + 7x - 5 = 0$ có hai nghiệm $x_{1},x_{2}$ nên theo Vi-ét ta có: $\left\{ \begin{array}{l} {x_{1} + x_{2} = - 7} \\ {x_{1}x_{2} = - 5} \end{array} \right.$

Và $x_{1}^{2} + 7x_{1} - 5 = 0$

Ta có: $P = \dfrac{x_{1}^{2} + x_{2}^{2}}{\left( {x_{1}^{2} + 7x_{1} - 6} \right)^{2025}} = \dfrac{\left( {x_{1} + x_{2}} \right)^{2} - 2x_{1}x_{2}}{\left\lbrack {\left( {x_{1}^{2} + 7x_{1} - 6} \right) - 1} \right\rbrack^{2025}} = \dfrac{{( - 7)}^{2} - 2 \cdot \left( {- 5} \right)}{{(0 - 1)}^{2025}} = \dfrac{59}{- 1} = - 59$.

Vậy $P = - 59$.

2) Theo đề bài, hàm số biểu thị mối liên hệ giữa độ cao ($h$) và áp suất khí quyển ($p$) là $p = a \cdot h + b$ với $a \neq 0,0 \leq h \leq 5000$

Tại $h = 0$ thì $p = 760$ nên ta có: $\left. 760 = a.0 + b\Leftrightarrow b = 760 \right.$

Tại $h = 2355$ thì $p = 571,6$ nên ta có: $2355a + b = 571,6$

Từ (1) và (2), ta có: $\left\{ \begin{array}{l} {b = 760} \\ {2355a + b = 571,6} \end{array}\Leftrightarrow\left\{ \begin{array}{l} {b = 760} \\ {2355a + 760 = 571,6} \end{array}\Leftrightarrow\left\{ \begin{array}{l} {b = 760} \\ {a = - 0,08} \end{array} \right. \right. \right.$

Khi đó, hàm số biểu thị mối liên hệ giữa độ cao ($h$) và áp suất khí quyển ($p$) là $p = - 0,08h + 760$

Áp suất khí quyển của vận động viên tại điểm dừng chân là $p = 540$, nên ta có $540 = - 0,08h + 760$

Suy ra, độ cao của vận động viên tại điểm dừng chân là $h = \dfrac{540 - 760}{- 0,08} = 2750\left( \text{m} \right)$

Vậy độ cao của điểm dừng chân so với mực nước biển là $h = 2750(m)$

PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link