Đánh giá năng lực Hà Nội
Đánh giá năng lực Hà Nội
Đường tròn
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Câu hỏi số 151:
Chứng minh rằng trong một đường tròn (O) nếu dây AB vuông góc với dây CD tại trung điểm I của CD thì dây AB là đường kính.
Bài 152:
Cho đường tròn (O ; R) trong đó có các dây AB, CD và DE với các đường vuông góc tương ứng OH, OI, OK.
Câu hỏi số 1:
Chứng minh rằng nếu AB = CD thì OH = OI và đảo lại
Câu hỏi số 2:
Chứng minh rằng nếu CD = DE thì tia Dx kẻ qua O là tia phân giác góc CDE.
Câu hỏi số 3:
Hai đường thẳng AB, DC cắt nhau tại M. Giả sử B nằm giữa A và M và C nằm giữa D và M. Chứng minh rằng nếu MB = MC thì AB = CD và đảo lại.
Câu hỏi số 4:
Dựng hình bình hành có hai đỉnh đã cho sao cho hai đỉnh còn lại nằm trên một đường tròn đã cho.
Bài 153:
Cho đường tròn (O) với hai dây song song AB và CD. Gọi các trung điểm của AB, CD lần lượt là I, K.
Câu hỏi số 1:
Chứng minh rằng I, K, O thẳng hàng.
Câu hỏi số 2:
So sánh AC với BD; AD với BC.
Câu hỏi số 3:
Chứng minh rằng nếu một đường tròn đi qua ba đỉnh của một hình thang cân thì cũng đi qua đỉnh còn lại.
Bài 154:
Cho một hình bình hành ABCD, I là giao điểm của hai đường chéo; đường tròn (O; R) đi qua ba điểm I, A, B và đường tròn (O'; R') đi qua 3 điểm I, C, D
Câu hỏi số 1:
So sánh R và R'
Câu hỏi số 2:
Ngoài điểm chung I, hai đường tròn (O ; R) và (O' ; R') còn điểm chung nào nữa không, tại sao?
Bài 155:
Cho bốn điểm A, B, C, D nằm trên cùng một đường thẳng theo thứ tự đó.
Câu hỏi số 1:
Hãy dựng đường tròn (O), (O1), (O2), (O3) có đường kính là AD, AB, BC, CD.
Câu hỏi số 2:
Chứng minh rằng mọi điểm nằm trên (O1), (O2), (O3) không kể hai điểm A và D đều nằm trong (O)
Câu hỏi số 3:
Chứng minh rằng mọi điểm nằm trên (O2) không kể hai điểm B và C đều nằm ngoài (O1) và (O2)
Câu hỏi số 156:
Cho một hình vuông ABCD, cạnh bằng a. Một đoạn thẳng MN có độ dài thay đổi, M chạy trên AB, N chạy trên AD sao cho chu vi tam giác AMN luôn luôn không đổi và bằng 2a. Gọi H là chân đường vuông góc hạ từ C xuống MN. Chứng minh rằng H luôn luôn nằm trên một đường tròn cố định
Bài 157:
Cho một đoạn thẳng cố định AB có độ dài bằng 2a. Gọi I là trung điểm của AB, K là trung điểm của IB. Trên tia Kx kẻ tùy ý, lấy một điểm M sao cho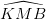 
= 
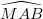
Câu hỏi số 1:
So sánh hai tam giác KMB và MAB
Câu hỏi số 2:
Tìm tập hợp điểm M
Câu hỏi số 3:
Dựng điểm M với a = 3 cm,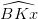 
= 1200 (không dùng thước đo góc )
Bài 158:
Cho đường tròn (O ; R) và một điểm M nằm trên ( O; R). Dựng điểm N sao cho MN vuông góc với OM đồng thời MN có độ dài bằng a cho trước
Câu hỏi số 1:
Tìm tập hợp điểm N
Câu hỏi số 2:
Tìm tập hợp chân đường vuông góc hạ từ M xuống ON
Câu hỏi số 3:
Tìm hệ thức giữa a và R để cho đường tròn (O; R) là tập hợp trọng tâm của ∆ MON
Bài 159:
Cho tam giác cân ABC (AB = AC), trung điểm I của BC, giao điểm H của các đường cao AD và CE
Câu hỏi số 1:
Chứng minh rằng các điểm D, E nằm trên đường tròn đường kính BC.
Câu hỏi số 2:
Chứng minh rằng bốn điểm A, B, I, D nằm trên cùng một đường tròn. Xác định tâm O và bán kính R của đường tròn đó rồi vẽ nó
Câu hỏi số 3:
Xác định tâm O' của đường tròn đi qua ba điểm C, D, H. Ngoài điểm D ra, hai đường tròn (O) và (O') có còn điểm nào chung nữa không ? Tại sao ?
Câu hỏi số 4:
Có nhận xét gì về góc giữa hai đường thẳng OO' và ID. Chứng minh điều đó
Câu hỏi số 5:
Chứng minh rằng bốn điểm O, I, O', D cùng nằm trên một đường tròn
Bài 160:
Cho ba dây AB, BC, CA của một đường tròn (O; r) trong đó AB là đường kính.
Câu hỏi số 1:
Chứng minh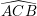 
= 900
Câu hỏi số 2:
Tìm tập hợp điểm I nhìn đoạn thẳng AB đã cho dưới một góc vuông.
Câu hỏi số 3:
Dựng tam giác vuông ABC có cạnh huyển AB cố định đã cho bằng 5 cm, cạnh góc vuông AC = 3 cm.
Câu hỏi số 4:
Dựng trực tâm của tam giác ABC có cạnh AB = 5cm, BC = 4,5 cm, CA = 4 cm.
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
