Đánh giá năng lực Hà Nội
Đánh giá năng lực Hà Nội
Đường tròn
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài 171:
Cho hình vuông ABCD có độ dài cạnh là a. Trong hình vuông đó lấy điểm K sao cho ∆ ABK đều. Các đường thẳng BK và AD cắt nhau tại P.
Câu hỏi số 1:
Tính độ dài đoạn thẳng KC theo a.
Câu hỏi số 2:
Trên đoạn thẳng AD lấy điểm I sao cho DI =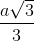 
, các đường thẳng CI và BP cắt nhau tại H. Chứng minh rằng tứ giác CHDP nội tiếp một đường tròn.
Câu hỏi số 3:
Gọi M và L lần lượt là trung điểm của các đoạn thẳng CP và KD.
Chứng minh rằng LM =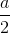 
.
Bài 172:
Cho tam giác ABC có ba góc nhọn và AB < AC. Vẽ đường cao AD và phân giác trong AO của tam giác ABC (D, O ϵ BC ). Vẽ đường tròn tâm O tiếp xúc với AB, AC lần lượt tại M và N.
Câu hỏi số 1:
Chứng minh các điểm M, N, O, D, A cùng thuộc một đường tròn.
Câu hỏi số 2:
Chứng minh rằng: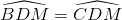 
Câu hỏi số 3:
Đường thẳng qua O và vuông góc với BC cắt MN tại I. Đường thẳng AI cắt đường thẳng BC tại K. Chứng minh rằng K là trung điểm của cạnh BC.
Bài 173:
Cho đường tròn (O) với đường kính AB = 2R. Trên đường thẳng tiếp xúc với đường tròn (O) tại A ta lấy điểm C sao cho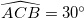 
. Gọi H là giao điểm thứ hai của đường thẳng BC với đường tròn (O).
Câu hỏi số 1:
Tính độ dài các đoạn thẳng AC, BC và khoảng cách từ A đến đường thẳng BC theo R
Câu hỏi số 2:
Với mỗi điểm M trên đoạn thẳng AC, đường thẳng BM cắt đường tròn (O) tại điểm N (khác B). Chứng minh rằng bốn điểm C, M, N, H nằm trên cùng một đường tròn và tâm của đường tròn đó luôn chạy trên một đường thẳng cố định khi M thay đổi trên đoạn thẳng AC.
Bài 174:
Cho đường tròn (O), M là một điểm nằm ngoài đường tròn (O). Qua M kẻ hai tiếp tuyến MA,MB đến đường tròn (O) với A,B là các tiếp điểm; MPQ là một cát tuyến không đi qua tâm của đường tròn (O), P nằm giữa M và Q. Qua P kẻ đường thẳng vuông góc với OA cắt AB, AQ tương ứng tại R,S. Gọi trung điểm đoạn PQ là N.
Câu hỏi số 1:
Chứng minh rằng: các điểm M, A, N, O, B cùng thuộc một đường tròn chỉ rõ bán kính của đường tròn đó.
Câu hỏi số 2:
Chứng minh rằng: PR = RS.
Bài 175:
Cho tam giác ABC có ba góc đều nhọn nội tiếp đường tròn tâm O, các đường cao BM và CN của tam giác cắt nhau tại H.
Câu hỏi số 1:
Chứng minh tứ giác BCMN là tứ giác nội tiếp trong một đường tròn.
Câu hỏi số 2:
Kéo dài AO cắt đường tròn (O) tại K. Chứng minh tứ giác BHCK là hình bình hành.
Câu hỏi số 3:
Cho cạnh BC cố định, A thay đổi trên cung lớn BC sao cho tam giác ABC luôn nhọn. Xác định vị trí điểm A để diện tích tam giác BCH lớn nhất.
Bài 176:
Cho đường tròn (O;R) có đường kính AB vuông góc với dây cung MN tại H (H nằm giữa O và B). Trên tia MN lấy điểm C nằm ngoài đường tròn (O;R) sao cho đoạn thẳng AC cắt đường tròn (O;R) tại điểm K khác A, hai dây MN và BK cắt nhau tại E.
Câu hỏi số 1:
Chứng minh rằng AHEK là tứ giác nội tiếp và ∆ CAE đồng dạng với ∆ CHK.
Câu hỏi số 2:
Qua N kẻ đường thẳng vuông góc với AC cắt tia MK tại F. Chứng minh ∆ NFK cân.
Câu hỏi số 3:
Giả sử KE = KC. Chứng minh: OK // MN và KM2 + KN2 = 4R2
Bài 177:
Cho đường tròn (O;R), dây cung BC cố định (BC < 2R) và điểm A di động trên cung lớn BC sao cho tam giác ABC có 3 góc nhọn. Các đường cao BD và CE của tam giác cắt nhau tại H.
Câu hỏi số 1:
Chứng minh tứ giác ADHE nội tiếp.
Câu hỏi số 2:
Giả sử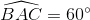 
, hãy tính khoảng cách từ tâm O đến cạnh BC theo R. Chứng minh đường thẳng kẻ qua A và vuông góc với DE luôn đi qua một điểm cố định.
Bài 178:
Cho nửa đường tròn tâm O đường kính AB. Điểm H cố định thuộc đường thẳng AO (H khác A và O). Đường thẳng đi qua điểm H và vuông góc với AO cắt nửa đường tròn (O) tại C. Trên cung BC lấy điểm D bất kì (D khác B và C). Tiếp tuyến của nửa đường tròn (O) tại D cắt đường thẳng HC tại E. Gọi I là giao điểm của AD và HC.
Câu hỏi số 1:
Chứng minh rằng tứ giác HBDI nội tiếp đường tròn.
Câu hỏi số 2:
Chứng minh tam giác DEI là tam giác cân.
Câu hỏi số 3:
Gọi F là tâm đường tròn ngoại tiếp tam giác ICD. Chứng minh góc ABF có số đo không đổi khi D thay đổi trên cung BC (D khác B và C).
Bài 179:
Cho đường tròn (O;R) và điểm M nằm ngoài sao cho OM = 2R. Đường thẳng d qua M tiếp xúc với (O;R) tại A. Gọi N là giao điểm của đoạn MO với đường tròn (O; R). Kẻ hai đường kính AB và CD khác nhau của (O; R). Các đường thẳng BC và BD cắt đường thẳng d lần lượt tại P và Q.
Câu hỏi số 1:
Tính độ dài đoạn thẳng AN theo R. Tính số đo của 
.
Câu hỏi số 2:
Chứng minh rằng: Tứ giác PQDC nội tiếp.
Câu hỏi số 3:
Chứng minh rằng: 3BQ - 2AQ > 4R.
Câu hỏi số 180:
Cho hai đường tròn (O; R) và (O'; R') có R= 6 cm; R' = 2 cm, OO' = 3 cm. Khi đó vị trí tương đối của hai đường tròn đã cho là:
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
