Đường tròn, Bài tập luyện chuyên đề Đường tròn

2K7! Học trực tuyến lớp 12 - Luyện Thi TN THPT, Đánh giá năng lực, Đánh giá tư duy
Cuộc thi viết Tri ân thầy cô ngày 20/11
Học trực tuyến lớp 10 các môn Toán - Lý - Hóa - Văn - Anh- Sinh-Sử-Địa cùng Thầy Cô giỏi, nổi tiếng
Học trực tuyến lớp 9 và luyện vào 10 cùng giáo viên nổi tiếng
Khoá học online trực tuyến cấp THCS năm học 2024 - 2025 | Tuyensinh247.com
2K7! Luyện đề Đánh giá năng lực, Đánh giá tư duy 2025
Học trực tuyến lớp 11 đủ môn cùng Thầy Cô giỏi, nổi tiếng
2K7! Luyện thi Đánh giá năng lực, Đánh giá tư duy 2025 (Lộ trình SUN 2025)|Tuyensinh247.com
2K8! Bứt Phá Lớp 11 2025! Học online trực tuyến lớp 11 Chương trình mới (VOD+LIVE)|Tuyensinh247.com
2K9! Bứt Phá Lớp 10! Học online trực tuyến lớp 10! Chương Trình Mới (VOD + LIVE)|Tuyensinh247.com
2K10! Học online trực tuyến lớp 9 và ôn thi vào 10 năm 2024-2025 | Tuyensinh247.com
Khoá học online trực tuyến cấp Tiểu học năm học 2024-2025 | Tuyensinh247.com
Khoá học online trực tuyến cấp Tiểu học và THCS năm học 2024-2025 | Tuyensinh247.com
Học online lớp 5 cùng thầy cô giáo giỏi, nổi tiếng
2K6! Thi thử Miễn Phí TN THPT 2024
Tuyensinh247 giải nóng đề thi vào lớp 10 năm 2024 - Tất cả các tỉnh
Học online lớp 7 cùng thầy cô giáo giỏi
Học online lớp 6 cùng thầy cô giỏi, nổi tiếng
Chương Trình Học Tốt Trung Học Cơ Sở Năm Học 2023-2024
Lộ Trình Học Bứt Phá Lớp 2-9 Năm Học 2023-2024
2K7! Bứt Phá Lớp 11 2024! Chương trình mới (VOD + LIVE)
Học online lớp 8 cùng thầy cô giáo giỏi
2K8! Bứt phá lớp 10! Chương trình mới (VOD + LIVE)
Chương trình học tốt tiểu học năm học 2023-2024
2K13! Bứt Phá Lớp 5 Năm Học 2023 - 2024
Học online lớp 4 cùng thầy cô giáo giỏi, nổi tiếng
Học online lớp 3 cùng thầy cô giáo giỏi, nổi tiếng
Học online lớp 2 với thầy cô giáo giỏi, nổi tiếng
2K6! Lộ Trình Sun 2024 - Ba bước luyện thi TN THPT - ĐH ít nhất 25 điểm
Khuyến Mãi Khoá Học 1K Chỉ Từ 11-13/09/2024
Khai giảng các khóa lớp 9 Toán - Lý - Hóa - Văn - Anh năm 2018
Khai giảng khóa Ngữ văn 7 - xây nền vững chắc cho tương lai!
Luyện thi vào lớp 10 môn Toán, Văn, Hóa, Anh, Lý với giáo viên giỏi và nổi tiếng

Bài tập luyện thêm - Luyện thi vào lớp 10 môn toán

Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!

Bài 251:

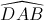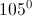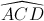Cho hình thang ABCD(AB//CD) nội tiếp đường tròn (C) tâm O, bán kính R và có $\widehat{DAB}$ = $105^{0}$ , $\widehat{ACD}$ = $30^{0}$ .

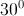Câu hỏi số 1: Chưa xác định

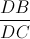Tính $\frac{DB}{DC}$ và tính AB theo R.

A. $AB=\sqrt{3}R$ , $\frac{DB}{DC}$ =1

B. $AB=\sqrt{2}R$ , $\frac{DB}{DC}$ =1

C. AB=R , $\frac{DB}{DC}$ =1

D. AB=1, $\frac{DB}{DC}$ =1

Xem lời giải

Câu hỏi: 17612

Câu hỏi số 2: Chưa xác định

Tiếp tuyến của (C) tại B cắt các đường thẳng DO,DA lần lượt tại M, N.Tính 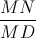$\frac{MN}{MD}$

A. $\frac{MN}{MD}=\frac{1}{4}$

B. $\frac{MN}{MD}=\frac{1}{3}$

C. $\frac{MN}{MD}=\frac{1}{2}$

D. $\frac{MN}{MD}=1$

Xem lời giải

Câu hỏi: 17613

Câu hỏi số 3: Chưa xác định

Gọi E là trung điểm của AB, tia DE cắt MN tại F. Tính 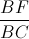$\frac{BF}{BC}$

A. $\frac{BF}{BC}=\frac{1}{2}$

B. $\frac{BF}{BC}=\frac{1}{3}$

C. $\frac{BF}{BC}=\frac{1}{4}$

D. $\frac{BF}{BC}=\frac{1}{5}$

Xem lời giải

Câu hỏi: 17614

Bài 252:

Cho đường tròn (O; R), dây CD có trung điểm H. Trên tia đối của tia DC lấy điểm S và qua S kẻ các tiếp tuyến SA, SB với đường tròn ; đường thẳng AB cắt SO, OH tại E và F. Chứng minh rằng:

Câu hỏi số 1: Chưa xác định

OE.OS = R².

A. Xét tam giác vuông SHF

B. Xét tam giác vuông SHO

C. Xét tam giác vuông SEF

D. Xét tam giác vuông SAO

Xem lời giải

Câu hỏi: 17586

Câu hỏi số 2: Chưa xác định

Tứ giác SEHF nội tiếp.

A. $\widehat{ESF}$ = 90^{0 ; = 90⁰}

B. $\widehat{SEF}$ = 90^{0 ; = 90⁰}

C. $\widehat{SEF}$ = 90^{0 ; = 90⁰}

D. $\widehat{SFE}$ = 90^{0 ; = 90⁰}

Xem lời giải

Câu hỏi: 17587

Câu hỏi số 3: Chưa xác định

Biết R = 10cm, OH = 6cm, SD = 4cm. Tính độ dài đoạn thẳng CD, SA.

A. CD = 6; SA = 3√5

B. CD = 12 ; SA = 4√5

C. CD = 9; SA = 4√5

D. CD = 12 (cm); SA = 7 (cm)

Xem lời giải

Câu hỏi: 17588

Bài 253:

Cho (O) và (O’) cắt nhau tại A và B. Các đường thẳng AO, AO’ cắt đường tròn (O) lần lượt tại C, D và cắt đường tròn (O’) tại E, F. Chứng minh rằng:

Câu hỏi số 1: Chưa xác định

C, B, F thẳng hàng.

A. AB ⊥AC; AB ⊥BF.

B. AB⊥BC; AB ⊥BF.

C. AB ⊥BF.

D. AB⊥BC.

Xem lời giải

Câu hỏi: 17564

Câu hỏi số 2: Chưa xác định

Tứ giác CDEF nội tiếp.

A. $\widehat{CFD}$ = $\widehat{CEF}$ = 90⁰

B. $\widehat{CDF}$ = $\widehat{CEF}$ = 90⁰

C. $\widehat{CDF}$ = $\widehat{CFE}$ = 90⁰

D. $\widehat{DCF}$ = $\widehat{CEF}$ = 90⁰

Xem lời giải

Câu hỏi: 17565

Câu hỏi số 3: Chưa xác định

A là tâm đường tròn nội tiếp tam giác BDE.

A. AD là phân giác của $\widehat{DEB}$ ; EA là phân giác của $\widehat{DEB}$

B. EA là phân giác của $\widehat{DEB}$

C. EA là phân giác của $\widehat{DEB}$ ;AD là phân giác của $\widehat{EDB}$ .

D. AD là phân giác của $\widehat{EDB}$

Xem lời giải

Câu hỏi: 17566

Bài 254:

Cho đường tròn (O; R) và điểm A ở ngoài (O). Vẽ tiếp tuyến AM, AN với (O). Đường thẳng chứa đường kính của đường tròn song song với MN cắt AM tại B, cắt AN tại C.

Câu hỏi số 1: Chưa xác định

Chứng minh I là tâm đường tròn nội tiếp tam giác AMN với I là giao điểm của AO với (O).

A. OB là phân giác $\widehat{AMN}$

B. OA là phân giác $\widehat{AMN}$

C. AI là phân giác $\widehat{MAN}$ ; OA là phân giác $\widehat{AMN}$

D. AI là phân giác $\widehat{MAN}$

Xem lời giải

Câu hỏi: 17544

Câu hỏi số 2: Chưa xác định

Chứng minh tứ giác MNCB là hình thang cân.

A. ∆BMN cân

B. ∆CMN cân

C. ∆DMN cân

D. ∆AMN cân

Xem lời giải

Câu hỏi: 17545

Câu hỏi số 3: Chưa xác định

Chứng minh MA.MB = R².

A. OA ⊥MB

B. BA ⊥MN

C. CA ⊥MN

D. OA ⊥MN

Xem lời giải

Câu hỏi: 17546

Câu hỏi số 4: Chưa xác định

Lấy D thuộc cung nhỏ MN. Vẽ tiếp tuyến qua D của (O) cắt AM, AN lần lượt tại P, Q. Chứng minh rằng PB.CQ = 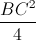$\frac{BC^{2}}{4}$ .

A. ∆PBO ̴ ∆OCQ.

B. ∆BPO ̴ ∆OCQ.

C. ∆PBO ̴ ∆COQ.

D. ∆POB ̴ ∆OCQ.

Xem lời giải

Câu hỏi: 17547

Bài 255:

Giải

Câu hỏi số 1: Chưa xác định

Rút gọn biểu thức; M = 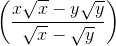$\left ( \frac{x\sqrt{x}-y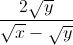\sqrt{y}}{\sqrt{x}-\sqrt{y}} \right )$ :(x-y) - $\frac{2\sqrt{y}}{\sqrt{x}-\sqrt{y}}$ với x>0; y>0, x 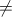$\neq$ y

A. M= x-y

B. M= $\frac{2\sqrt{y}}{\sqrt{x}-\sqrt{y}}$

C. M= $\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x}-\sqrt{y}}$

D. M = 1

Xem lời giải

Câu hỏi: 17526

Câu hỏi số 2: Chưa xác định

Người ta làm một vườn hoa gồm 2 hình tròn tâm A và B tiếp xúc ngoài với nhau. Biết AB = 5cm và diện tích vườn hoa là 13,48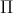 $\Pi$ m ². Tính bán kính của mỗi hình tròn.

A. Bán kính của 2 đường tròn là 3,5m và 1,5 m.

B. Bán kính của 2 đường tròn là 3,8m và 1,2 m.

C. Bán kính của 2 đường tròn là 3,6m và 1,4 m.

D. Bán kính của 2 đường tròn là 3,2m và 1,8 m.

Xem lời giải

Câu hỏi: 17527

Câu hỏi số 3: Chưa xác định

Giải hệ phương trình: 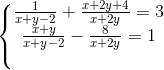$\left\{\begin{matrix} \frac{1}{x+y-2}+\frac{x+2y+4}{x+2y}=3\\ \frac{x+y}{x+y-2}-\frac{8}{x+2y} = 1 \\ \\ \end{matrix}\right.$

A. Hệ phương trình có nghiệm (x=- 2, y = 1)

B. Hệ phương trình có nghiệm (x= 2, y = -1)

C. Hệ phương trình có nghiệm (x=-2, y = -1)

D. Hệ phương trình có nghiệm (x= 2, y = 1)

Xem lời giải

Câu hỏi: 17528

Bài 256:

Cho đường tròn (O) có tâm O và đường tròn (I) có tâm I, chúng cắt nhau tại hai điểm phân biệt A và B ( O và I nằm khác phía đối với đường thẳng AB). Đường thẳng IB cắt (O) tại điểm thứ 2 là F. Đường thẳng qua B song song với EFcắt (O) tại N.

Câu hỏi số 1: Chưa xác định

Chứng minh: Tứ giác AOEF nội tiếp.

A. $\widehat{EOF}=\widehat{EAF}=\widehat{EFI}$

B. $\widehat{EOF}=\widehat{EAF}=\widehat{EIF}$

C. $\widehat{EOF}=\widehat{EFA}=\widehat{EIF}$

D. $\widehat{EFO}=\widehat{EAF}=\widehat{EIF}$

Xem lời giải

Câu hỏi: 17493

Câu hỏi số 2: Chưa xác định

Chúng minh : MN=AE+EF

A. AE+AF=MA+AN=MN.

B. AE+AF=MI+IN=MN.

C. AE+AF=MB+BN=MN.

D. AE+AF=MC+CN=MN.

Xem lời giải

Câu hỏi: 17494

Bài 257:

Cho đường tròn (O) có tâm O và điểm M nằm ngoài đường tròn (O). Đường thẳng MO cắt (O) tại E và F (ME<MF). Vẽ cát tuyến MAB và tiếp tuyến MC của (O) (C là tiếp điểm , A nằm giữa hai điểm M và B, A và C nằm khác phía với đường thẳng MO)

Câu hỏi số 1: Chưa xác định

Chứng minh rằng : MA.MB=ME.MF

A. $\Delta$ MEA $\sim$ $\Delta$ MBF

B. $\Delta$ MEA $\sim$ $\Delta$ MFB

C. $\Delta$ MAE $\sim$ $\Delta$ MBF

D. $\Delta$ EMA $\sim$ $\Delta$ MBF

Xem lời giải

Câu hỏi: 17334

Câu hỏi số 2: Chưa xác định

Gọi H là hình chiếu vuông góc của điểm C lên đường thằng MO.Chứng minh tứ giác AHOB nội tiếp.

A. $\widehat{MAH}=\widehat{MBO}$

B. $\widehat{MAH}=\widehat{MBO}$

C. $\widehat{MHA}=\widehat{MBO}$

D. $\widehat{MHA}=\widehat{MBO}$

Xem lời giải

Câu hỏi: 17335

Câu hỏi số 3: Chưa xác định

Trên nửa mặt phẳng bờ OM có chứa điểm A, vẽ nửa đường tròn đường kính MF; nửa đường tròn này cắt tiếp tuyến tại E của (O) ở K.Gọi S là giao điểm của hai đường thẳng CO và KF.Chứng minh rằng đường thẳng MS vuông góc với đường thẳng KC.

A. MS là đường trung trực KC

B. MS =KC

C. MS = $\frac{1}{2}$ KC

D. MS là đường thẳng qua trung điểm KC

Xem lời giải

Câu hỏi: 17336

Câu hỏi số 4: Chưa xác định

Gọi P và Q lần lượt là tâm đường tròn ngoại tiếp tam giác EFS và ABS và T là trung điểm của KS. Chúng minh ba điểm P,Q,T thẳng hàng.

A. PQ là đường trung trực của đoạn thẳng SI, mà T không thuộc SI

B. PQ là đường trung trực của đoạn thẳng SI, mà T là trung điểm

C. PQ là đường trung trực của đoạn thẳng SI, mà T thuộc đường trung trực của đoạn thẳng SI

D. PQ là đường trung trực của đoạn thẳng SI, mà T nằm trên SI

Xem lời giải

Câu hỏi: 17337

Bài 258:

Cho tam giác ABC nhọn nội tiếp (O). Tia phân giác góc B cắt (O) tại D, tia phân giác góc c cắt (O) tại E, hai tia này cắt nhau tại F. Gọi I,K theo thứ tự là hai giao điểm của dây cung DE với AB, AC.

Câu hỏi số 1: Chưa xác định

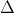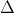Chứng minh $\Delta$ EBF , $\Delta$ DAF là các tam giác cân.

A. $\widehat{EBF}$ = $\widehat{EFB}$ ; $\widehat{AFD }$ = $\widehat{DFC}$

B. $\widehat{EBF}$ = $\widehat{EFB}$ ; $\widehat{AFD }$ = $\widehat{ADF}$

C. $\widehat{EBF}$ = $\widehat{BEF}$ ; $\widehat{AFD }$ = $\widehat{FAD}$

D. $\widehat{EBF}$ = $\widehat{EFB}$ ; $\widehat{AFD }$ = $\widehat{FAD}$

Xem lời giải

Câu hỏi: 17308

Câu hỏi số 2: Chưa xác định

Chứng minh tứ giác DKFC nội tiếp và FK//AB.

A. $\widehat{FKC}$ = $\widehat{FAB}$

B. $\widehat{FAD}$ = $\widehat{FAB}$

C. $\widehat{FKC}$ = $\widehat{FAD}$

D. $\widehat{FKC}$ = $\widehat{FKA}$

Xem lời giải

Câu hỏi: 17309

Câu hỏi số 3: Chưa xác định

Tứ giác AIFK là hình gì?Vì sao?

A. Tứ giác AIFK là hình bình hành

B. Tứ giác AIFK là hình thang cân

C. Tứ giác AIFK là hình chư nhật

D. Tứ giác AIFK là hình thoi

Xem lời giải

Câu hỏi: 17310

Câu hỏi số 4: Chưa xác định

Tìm điều kiện của tam giác ABC để tứ giác AEFD là hình thoi.

A. Tam giác ABC là tam giác cân

B. Tam giác ABC là tam giác vuông

C. Tam giác ABC là tam giác đều

D. Tam giác ABC là tam giác vuông cân

Xem lời giải

Câu hỏi: 17311

Bài 259:

Cho đường tròn (O) , đường kính AB = 2R và một điểm C trên đường tròn. Trên nửa mặt phẳng bờ AB có chứa đểm C, kẻ tia Ã tiếp xúc với (O). Gọi M là điểm chính giữa 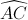$\widehat{AC}$ nhỏ. AC cắt BM tại P. Tia BC cắt AM, Ax lần lượt tại N và Q.

Câu hỏi số 1: Chưa xác định

Chứng minh rằng tam giác ABN cân.

A. BM vuông góc với AN , $\widehat{ABM}$ = $\widehat{MBN}$

B. BM vuông góc với AQ, $\widehat{ABM}$ = $\widehat{MBN}$

C. BM vuông góc với AC, $\widehat{ABM}$ = $\widehat{MBN}$

D. BM vuông góc với AB, $\widehat{ABM}$ = $\widehat{MBN}$

Xem lời giải

Câu hỏi: 17252

Câu hỏi số 2: Chưa xác định

Tứ giác APNQ là hình gì ? Vì sao?

A. Tứ giác APNQ là hình chữ nhật

B. Tứ giác APNQ là hình bình hành

C. Tứ giác APNQ là hình thang

D. Tứ giác APNQ là hình thoi

Xem lời giải

Câu hỏi: 17253

Câu hỏi số 3: Chưa xác định

Xác định vị trí của C để đường trong ngoại tiếp tam giác MNQ tiếp xúc (O)

A. BC = $\frac{1}{3}$ QB.

B. C là trung điểm QB.

C. C tùy ý.

D. C $\equiv$ M

Xem lời giải

Câu hỏi: 17254

Bài 260:

Cho nửa đường tròn tròn đường kính AB, trên đó có 1 điểm M. Trên đường kính AB có 1 điểm C sao cho AC<CB. Trên nửa mặt phẳng bờ AB có chứa điểm M, kẻ Ax, By vuông góc với AB.Đường thẳng qua M vuông góc với MC cắt Ax tại P, đường thẳng qua C vuông góc vơi CP cắt By tại Q. CP cắt AM tại D; CQ cắt BM tại E.

Câu hỏi số 1: Chưa xác định

Chứng minh rằng: Các tứ giác ACMP, CDME nội tiếp.

A. $\widehat{PAC}$ = $\widehat{CMP}$ = 90⁰ $\widehat{DCE}$ = $\widehat{DME}$ =180⁰