Đánh giá năng lực Hà Nội
Đánh giá năng lực Hà Nội
Đường tròn
Lưu ý: Chức năng này hiện không còn dùng nữa, vui lòng chọn các khóa học để xem các bài giảng hoặc làm đề thi online!
Bài 41:
Cho tam giác ABC vuông tại A, M là một điểm thuộc cạnh AC (M khác A và C ). Đường tròn đường kính MC cắt BC tại N và cắt tia BM tại I.
Câu hỏi số 1:
Chứng minh rằng: ABNM và ABCI là các tứ giác nội tiếp đường tròn.
Câu hỏi số 2:
Chứng minh rằng: NM là tia phân giác của góc 
Câu hỏi số 3:
Chứng minh rằng: BM.BI + CM.CA = AB2 + AC2.
Bài 42:
Cho đường tròn (O;R); AB và CD là hai đường kính khác nhau của đường tròn. Tiếp tuyến tại B của đường tròn (O;R) cắt các đường thẳng AC, AD thứ tự tại E và F.
Câu hỏi số 1:
Chứng minh tứ giác ACBD là hình chữ nhật.
Câu hỏi số 2:
Chứng minh ∆ACD ~ ∆CBE
Câu hỏi số 3:
Chứng minh tứ giác CDFE nội tiếp được đường tròn.
Câu hỏi số 4:
Gọi S, S1, S2 thứ tự là diện tích của ∆AEF, ∆BCE và ∆BDF. Chứng minh: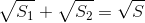
Bài 43:
Cho hình vuông ABCD có hai đường chéo cắt nhau tại E. Lấy I thuộc cạnh AB, M thuộc cạnh BC sao cho: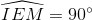 
(I và M không trùng với các đỉnh của hình vuông ).
Câu hỏi số 1:
Chứng minh rằng BIEM là tứ giác nội tiếp đường tròn
Câu hỏi số 2:
Tính số đo của góc 
Câu hỏi số 3:
Gọi N là giao điểm của tia AM và tia DC; K là giao điểm của BN và tia EM. Chứng minh CK ┴ BN.
Bài 44:
Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O;R). Các đường cao BE và CF cắt nhau tại H.
Câu hỏi số 1:
Chứng minh: AEHF và BCEF là các tứ giác nội tiếp đường tròn.
Câu hỏi số 2:
Gọi M và N thứ tự là giao điểm thứ hai của đường tròn (O;R) với BE và CF. Chứng minh: MN // EF.
Câu hỏi số 3:
Chứng minh rằng OA ┴ EF.
Bài 45:
Từ một điểm A nằm ngoài đường tròn (O;R) ta vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Trên cung nhỏ BC lấy một điểm M, vẽ MI ┴ AB, MK ┴ AC (I ϵ AB, K ϵ AC).
Câu hỏi số 1:
Chứng minh: AIMK là tứ giác nội tiếp đường tròn.
Câu hỏi số 2:
Vẽ MP ┴ BC (P ϵ BC). Chứng minh: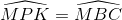 
Câu hỏi số 3:
Xác định vị trí của điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị lớn nhất.
Bài 46:
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I (I nằm giữa A và O ). Lấy điểm E trên cung nhỏ BC ( E khác B và C ), AE cắt CD tại F. Chứng minh:
Câu hỏi số 1:
BEFI là tứ giác nội tiếp đường tròn.
Câu hỏi số 2:
AE.AF = AC2
Câu hỏi số 3:
Khi E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp ∆CEF luôn thuộc một đường thẳng cố định.
Bài 47:
Cho đường tròn (O; R) đường kính AC. Trên bán kính OA lấy điểm B tùy ý (B khác O và A). Vẽ đường tròn (N) tâm N đường kính AB. Gọi M là trung điểm của đoạn BC. Qua M vẽ dây cung DE vuông góc với BC, AD cắt (N) tại I.
Câu hỏi số 1:
Chứng minh tứ giác BMDI nội tiếp.
Câu hỏi số 2:
Chứng minh 3 điểm I, B, E thẳng hàng.
Câu hỏi số 3:
Chứng minh MI là tiếp tuyến của (N).
Câu hỏi số 4:
Đường tròn tâm D bán kính DM cắt (O) tại P và Q. Chứng minh PQ đi qua trung điểm của đoạn MD.
Bài 48:
Từ điểm A nằm ngoài đường tròn (O; R) vẽ tiếp tuyến AB và AC đến (O), (B, C là tiếp điểm). Vẽ đường thẳng qua C và vuông góc với AB tại H, CH cắt (O) tại E và cắt OA tại D.
Câu hỏi số 1:
Chứng minh tam giác OCD cân.
Câu hỏi số 2:
Gọi M là trung điểm của đoạn CE, OM cắt AC tại K. Chứng minh: - BM đi qua trung điểm của OH. - Tứ giác OEKC nội tiếp.
Câu hỏi số 3:
Khi OA = 2R. Tính theo R phần diện tích tứ giác OBAC nằm ngoài (O).
Bài 49:
Cho đường tròn tâm O bán kính R. Từ một điểm S nằm ngoài đường tròn (O) vẽ hai tiếp tuyến SA, SB với đường tròn (O) (A, B là hai tiếp điểm) và cát tuyến Sx cắt đường tròn lần lượt tại M, N.
Câu hỏi số 1:
Chứng minh SO ┴ AB.
Câu hỏi số 2:
Gọi H là giao điểm của SO và AB, I là trung điểm của MN. Hai đường thẳng OI, AB cắt nhau tại E. Chứng minh: OI.OE = R2
Câu hỏi số 3:
Biết SO = 2R, MN = 
. Tính diện tích tam giác ESM theo R.
Bài 50:
Cho điểm A nằm ngoài đường tròn (O; R). Từ A kẻ đường thẳng d bất kì không đi qua điểm O và cắt (O) tại B, C (AB < AC). Các tiếp tuyến của (O) tại B và C cắt nhau tại D. Kẻ DH vuông góc AO tại H, DH cắt cung nhỏ BC tại M. Gọi I là giao điểm của DO và BC
Câu hỏi số 1:
Chứng minh rằng ngũ giác DBHOC và tứ giác DIHA nội tiếp.
Câu hỏi số 2:
Chứng minh: AM là tiếp tuyến của (O).
Câu hỏi số 3:
Chứng minh: HB, HC không đổi khi quay quanh A.
Còn hàng ngàn bài tập hay, nhanh tay thử sức!
>> Luyện thi tốt nghiệp THPT và Đại học, mọi lúc, mọi nơi tất cả các môn cùng các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu trên Tuyensinh247.com.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
