Một cốc nước có dạng hình trụ có bán kính đáy bằng \(3cm\), chiều cao \(12cm\) và chứa một

Câu hỏi số 214335:

Vận dụng

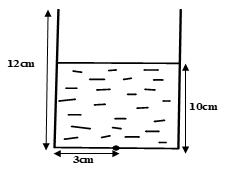
Một cốc nước có dạng hình trụ có bán kính đáy bằng \(3cm\), chiều cao \(12cm\) và chứa một lượng nước cao \(10cm\). Người ta thả từ từ \(3\) viên bi làm bằng thủy tinh có đường kính bằng \(2cm\) vào cốc nước. Hỏi mực nước trong cốc lúc này cao bao nhiêu?

A. \(\dfrac{{100}}{9}cm\)

B. \(\dfrac{{94}}{9}cm\)

C. \(\dfrac{{74}}{3}cm\)

D. \(\dfrac{{50}}{9}cm\)

Đáp án đúng là: B

Quảng cáo

Xem lời giải

Câu hỏi:214335

Phương pháp giải

Ở bài toán này cũng có sử dụng kiến thức Vật Lý 6:

“ Khi cho một vật rắn (không thấm nước) vào một bình chia độ ( hay một cái li, cái chén,…) mà nước (hoặc các chất lỏng như dầu, rượu,…) không bị tràn ra ngoài, thì thể tích phần nước dâng lên trong bình sau khi bỏ vật chính là thể tích của vật”.

Giải chi tiết

Bài giải chi tiết:

Bán kính của viên bi là: \(R = \dfrac{d}{2} = \dfrac{2}{2} = 1cm\)

Thể tích của một viên bi là: \({V_1} = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.1^3} = \dfrac{4}{3}\pi \left( {c{m^3}} \right)\)

Do ba viên bi có cùng đường kính nên tổng thể tích của 3 viên bi là: \(V = 3.{V_1} = 3.\dfrac{4}{3}\pi = 4\pi \left( {c{m^3}} \right)\)

Diện tích của đáy cốc nước (hình tròn \(r = 3cm\)): \(S = \pi .{r^2} = \pi {.3^2} = 9\pi \left( {c{m^2}} \right)\)

Chiều cao của phần cốc mà không chứa nước: \(h = 12 - 10 = 2cm\)

Thể tích phần cốc không chứa nước ( cốc hình trụ, diện tích phần đáy cũng là diện tích phần mặt phân cách giữa phần có nước và phần không có nước)

\(V' = S.h = 9\pi .2 = 18\pi \left( {c{m^3}} \right)\)

Do: \(V' > V\) nên khi thả \(3\) viên bi vào li nước thì nước không bị tràn ra ngoài,

Gọi \(x\) là chiều cao mực nước dâng lên sau khi thả \(3\) viên bi vào cốc, thể tích của \(3\) viên bi cũng là thể tích phần nước dâng lên nên ta có phương trình:

\(V = S.x \Leftrightarrow 9\pi .x = 4\pi \Leftrightarrow x = \dfrac{4}{9}cm\)

Vậy: Chiều cao của mực nước trong ống sau khi thả \(3\) viên bi là: \(10 + \dfrac{4}{9} = \dfrac{{94}}{9}cm\)

Chú ý khi giải

Bình luận về bài toán:

Đây có thể là một bài toán không khó với một số em, nhưng tôi chắc chắn rằng để lấy được 1 điểm trọn vẹn đối với bài toán này thì rất ít bạn làm được.

Phần mất điểm đối với hầu hết các em là “quên” đi tính phần thể tích không chứa nước trong cái li (“phần thể tích còn trống”), bởi nếu, các em không tính phần thể tích đó, mà chỉ tính tổng thể tích của 3 viên bi bỏ vào li, nếu như, đề “gài bẫy” để cho tổng thể tích 3 viên bi bỏ vào lớn hơn thể tích mà chiếc li còn trống thì khi bỏ 3 viên bi vào nước sẽ tràn ra ngoài. Lúc đó, chiều cao mực nước sau khi bỏ 3 viên bi sẽ là chiều cao của chiếc li, tức là \(12cm\).

Còn một số em tính trực tiếp được mực nước dâng lên sau khi bỏ 3 viên bi vào là \(\dfrac{{94}}{9}cm < 12cm\) rồi mới đi lập luận nước không tràn ra ngoài sau khi bỏ 3 viên bi vào. Như vậy, là không chặt chẽ. Nếu nước tràn ra ngoài mà không lập luận như trên thì làm sao ra được kết quả \(< 12cm\)?

Đáp án cần chọn là: B

PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link