Ngọn Hải đăng Kê Gà ở tỉnh Bình Thuận là ngọn tháp thắp đèn gần bờ biển

Câu hỏi số 228610:

Vận dụng

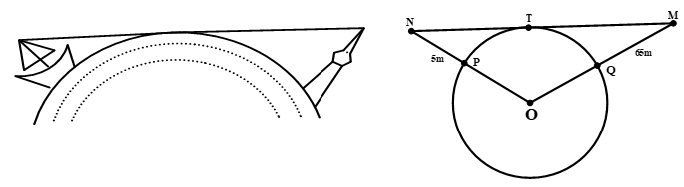
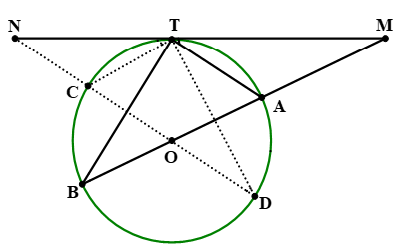
Ngọn Hải đăng Kê Gà ở tỉnh Bình Thuận là ngọn tháp thắp đèn gần bờ biển dùng để định hướng cho tàu thuyền giao thông trong khu vực vào ban đêm. Đây là ngọn Hải đăng được xem là cổ xưa và cao nhất Việt Nam. Chiều cao của ngọn đèn so với mặt nước biển là 65m. Hỏi:

a) Một người quan sát đứng tại vị trí đèn của Hải đăng nhìn xa tối đa bao nhiêu trên mặt biển?

b) Cách bao xa thì một người quan sát đứng ở trên tàu bắt đầu trông thấy ngọn đèn này, biết rằng mắt người quan sát đứng ở trên tàu có độ cao 5m so với mặt nước biển?
(Cho biết bán kính Trái Đất gần bằng 6400km và điều kiện quan sát trên biển là không bị che khuất)

Quảng cáo

Xem lời giải

Câu hỏi:228610

Giải chi tiết

a) Người quan sát đứng tại vị trí đèn của Hải đăng nhìn xa tối đa trên mặt biển một đoạn tương ứng với MT.

MN tiếp xúc với đường tròn (O) tại T nên MN là tiếp tuyến đường tròn (O). Xét tam giác ATM và tam giác TAM, ta có:

Góc AMT chung.

Góc ATM = góc TBM (cùng chắn cung nhỏ AT).

Chú thích:

+) góc ATM = \(\frac{1}{2}\)sđ cung nhỏ AT (góc tạo bởi tiếp tuyến với dây cung).

+) góc TBM = \(\frac{1}{2}\)sđ cung nhỏ AT (góc nội tiếp có đỉnh nằm trên đường tròn).

\(\Rightarrow \Delta ATM\) đồng dạng \(\Delta TBM\)(g-g).

\(\begin{array}{l} \Rightarrow \frac{{TM}}{{BM}} = \frac{{AM}}{{TM}}\\ \Leftrightarrow T{M^2} = AM.BM\\ \Leftrightarrow T{M^2} = AM.\left( {AM + AB} \right)\\ \Leftrightarrow T{M^2} = AM.\left( {AM + 2R} \right)\end{array}\)

Thay số, ta có:

\(\begin{array}{l}T{M^2} = 0,065.\left( {0,065 + 2.6400} \right)\left( {AM = 65m = 0,065km} \right)\\ \Leftrightarrow TM \approx 29km\end{array}\)

Vậy: Một người quan sát đứng tại vị trí đèn của Hải đăng nhìn xa tối đa khoảng 29km.

b) NO cắt đường tròn (O) tại hai điểm C và D, với C nằm giữa 2 điểm N và O.

Cách một khoảng MN thì người quan sát đứng ở trên tàu bắt đầu trông thấy ngọn đèn của Hải Đăng. Chứng minh tương tự như trên, ta có:

\(\Rightarrow \Delta CTN\) đồng dạng \(\Delta TDN\) (g-g)

\(\begin{array}{l} \Rightarrow \frac{{TN}}{{DN}} = \frac{{CN}}{{TN}}\\ \Leftrightarrow T{N^2} = CN.DN\\ \Leftrightarrow T{N^2} = CN.\left( {CN + CD} \right)\\ \Leftrightarrow T{N^2} = CN.\left( {CN + 2R} \right)\end{array}\)

Thay số, ta có:

\(\begin{array}{l}T{N^2} = 0,005.\left( {0,005 + 2.6400} \right)\left( {CN = 5m = 0,005km} \right)\\ \Leftrightarrow TN \approx 8km\end{array}\)

\(MN=MT+TN=29+8=37km\)

Vậy: Cách khoảng 37km thì một người quan sát đứng ở trên tàu bắt đầu trông thấy ngọn đèn của Hải Đăng .

PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!

Câu hỏi trước Câu tiếp theo

>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link