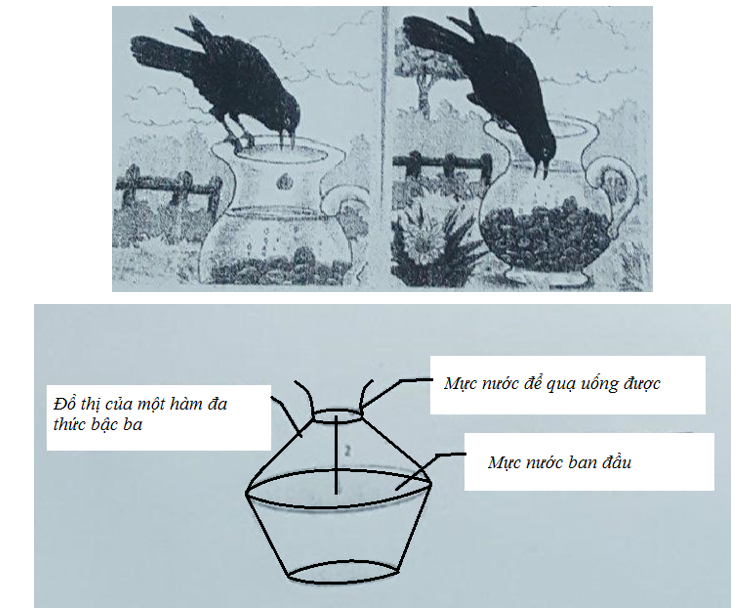
Một con quạ đang khát nước, nó tìm thấy một cái lọ có nước nhưng cổ lọ lại cao không thò

Câu hỏi số 247813:

Vận dụng cao

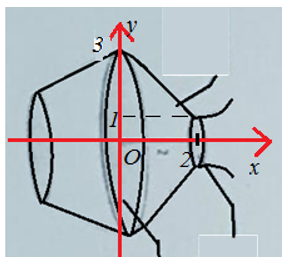
Một con quạ đang khát nước, nó tìm thấy một cái lọ có nước nhưng cổ lọ lại cao không thò mỏ vào uống được. Nó nghĩ ra một cách, nó gắp từng viên bi (hình cầu) bỏ vào trong lọ để nước dâng lên mà tha hồ uống. Hỏi con quạ cần bỏ vào lọ ít nhất bao nhiêu viên để có thể uống nước? Biết rằng mỗi viên bi có bán kính là \(\frac{3}{4}\)(đvđd) và không thấm nước, cái lọ có hình dáng là một khối tròn xoay với đường sinh là một hàm đa thức bậc ba, mực nước bạn đầu trong lọ ở vị trí mà mặt thoáng tạo thành hình tròn có bán kính lớn nhất \(R=3\), mực nước quạ có thể uống là vị trí mà hình tròn có bán kính nhỏ nhất \(r=1\) và khoảng cách giữa 2 mặt này bằng 2, được minh họa như hình vẽ sau:

A. 17

B. 16

C. 15

D. 18

Đáp án đúng là: B

Quảng cáo

Xem lời giải

Câu hỏi:247813

Phương pháp giải

- Gắn hệ trục tọa độ Oxy, xác định phương trình hàm số bậc ba.

- Ứng dụng tích phân vào tính thể tích.

Giải chi tiết

Gắn hệ trục tọa độ Oxy như hình vẽ.

Gọi phương trình của đường sinh là: \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\,\,\,(C),\,\,a\ne 0\)

Theo đề bài, ta có: (C) có điểm cực đại \((0;3)\), điểm cực tiểu là \((2;1)\).

\(\Rightarrow \left\{ \begin{align} & 3=d\,\,\,\,(1) \\ & 1=8a+4b+2c+3\,\,\,\,(2) \\\end{align} \right.\)

\(y'=3a{{x}^{2}}+2bx+c\) \(\Rightarrow \left\{ \begin{align} & c=0\,\,\,\,(3) \\ & 12a+4b+c=0\,\,(4) \\\end{align} \right.\)

Từ (1),(2),(3) và (4) \(\Rightarrow \left\{ \begin{align} & a=\frac{1}{2} \\ & b=-\frac{3}{2} \\ & c=0 \\ & d=3 \\\end{align} \right.\Rightarrow (C):y=\frac{1}{2}{{x}^{3}}-\frac{3}{2}{{x}^{2}}+3\)

Thể tích đá cho vào: \(V=\pi \int\limits_{0}^{2}{{{\left( \frac{1}{2}{{x}^{3}}-\frac{3}{2}{{x}^{2}}+3 \right)}^{2}}dx}=\frac{314\pi }{35}\)

Thể tích 1 viên bi là: \({{V}_{bi}}=\frac{4}{3}\pi {{r}_{bi}}^{3}=\frac{4}{3}\pi {{\left( \frac{3}{4} \right)}^{3}}=\frac{9\pi }{16}\)

Cần số viên bi: \(\frac{\frac{314\pi }{35}}{\frac{9\pi }{16}}\approx 16\) (viên).

Đáp án cần chọn là: B

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.