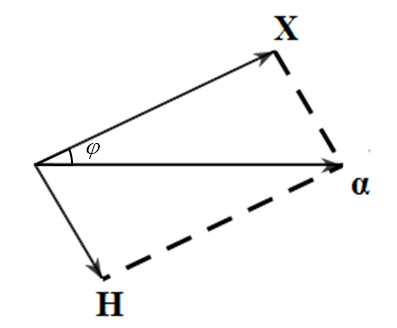
Dùng hạt \(\alpha \) có động năng \(5\,\,MeV\) bắn vào hạt nhân \({}_7^{14}N\) đứng yên gây ra
Dùng hạt \(\alpha \) có động năng \(5\,\,MeV\) bắn vào hạt nhân \({}_7^{14}N\) đứng yên gây ra phản ứng \({}_2^4He + {}_7^{14}N \to X + {}_1^1H\). Phản ứng thu năng lượng \(1,21\,\,MeV\) và không kèm theo bức xạ gamma. Lấy khối lượng các hạt nhân tính theo đơn vị u bằng số khối của chúng. Hạt nhân \(X\) bay ra theo hướng lệch với hướng chuyển động của hạt \(\alpha \) một góc lớn nhất gần với giá trị nào sau đây nhất?
Đáp án đúng là: B
Quảng cáo
Định luật bảo toàn động lượng: \(\overrightarrow {{p_\alpha }} + \overrightarrow {{p_N}} = \overrightarrow {{p_X}} + \overrightarrow {{p_H}} \)
Định luật bảo toàn năng lượng toàn phần: \(\Delta E + {K_\alpha } + {K_N} = {K_X} + {K_H}\)
Mối liên hệ giữa động năng và động lượng: \({p_X}^2 = 2{m_X}{K_X}\)
Định lí hàm cos: \({a^2} = {b^2} + {c^2} - 2bc{\mathop{\rm cosA}\nolimits} \)
Ta có phương trình phản ứng:
\({}_2^4He + {}_7^{14}N \to {}_8^{17}X + {}_1^1H\)
Phản ứng thu năng lượng \( \Rightarrow \Delta E = - 1,21\,\,\left( {MeV} \right)\)
Áp dụng định luật bảo toàn năng lượng toàn phần, ta có:
\(\begin{array}{l}
\Delta E + {K_\alpha } = {K_X} + {K_H}\\
\Rightarrow - 1,21 + 5 = {K_X} + {K_H} = 3,79\,\,\left( {MeV} \right)\\
\Rightarrow {K_H} = 3,79 - {K_X}
\end{array}\)
Ta có hình vẽ:
Từ hình vẽ, áp dụng công thức định lí hàm cos, ta có:
\(\begin{array}{*{20}{l}}
{{p_H}^2 = {p_X}^2 + {p_\alpha }^2 - 2{p_X}{p_\alpha }\cos \varphi }\\
{ \Rightarrow 2{m_H}{K_H} = 2{m_X}{K_X} + 2{m_\alpha }{K_\alpha } - 2\sqrt {2{m_X}{K_X}.2{m_\alpha }{K_\alpha }} .cos\varphi }\\
{ \Rightarrow {K_H} = 17{K_X} + 4.5 - 2\sqrt {17{K_X}.4.5} \cos \varphi }\\
{ \Rightarrow 3,79 - {K_X} = 17{K_X} + 20 - 2\sqrt {340{K_X}} \cos \varphi }\\
{ \Rightarrow 340{K_X}{{\cos }^2}\varphi = {{\left( {9{K_X} + 8,105} \right)}^2}}\\
{ \Rightarrow 81{K_X}^2 + \left( {145,89 - 340{{\cos }^2}\varphi } \right){K_X} + 8,{{105}^2} = 0\,\,\left( 1 \right)}
\end{array}\)
Xét \(\Delta = {\left( {145,89 - 340{{\cos }^2}\varphi } \right)^2} - 4.81.8,{105^2}\)
Để phương trình (1) có nghiệm, ta có: \(\Delta \ge 0\)
\(\begin{array}{l}
\Rightarrow {\left( {145,89 - 340{{\cos }^2}\varphi } \right)^2} \ge 145,{89^2}\\
\Rightarrow 145,89 - 340{\cos ^2}\varphi \le - 145,89\\
\Rightarrow {\cos ^2}\varphi \ge 0,858 \Rightarrow \cos \varphi \ge 0,926 \Rightarrow \varphi \le {22^0}
\end{array}\)
Đáp án cần chọn là: B
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
