Cho hàm số \(y = {x^2} - 4x + m\) a) Lập bảng biến thiên và vẽ đồ thị hàm số trên với
Cho hàm số \(y = {x^2} - 4x + m\)
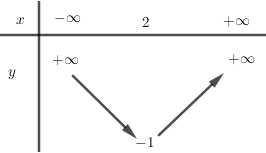
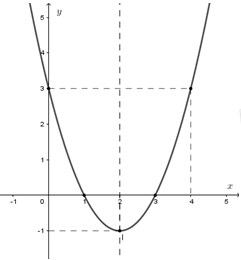
a) Lập bảng biến thiên và vẽ đồ thị hàm số trên với \(m = 3.\)
b) Tìm \(m\) sao cho đồ thị cắt \(Ox\) tại \(2\) điểm phân biệt \(A,\,B\) với \(OA = 3OB.\)
Đáp án đúng là: C
Quảng cáo
a) Tìm trục đối xứng, đỉnh, khoảng đồng biến nghịch biến, lập bảng biến thiên.
Tìm tọa độ các điểm đi qua và vẽ đồ thị.
b) Tìm điều kiện để phương trình có hai nghiệm phân biệt.
- Tìm hai nghiệm và suy ra tọa độ, dùng điều kiện \(OA = 3OB\) tìm \(m\).
a) Lập bảng biến thiên và vẽ đồ thị hàm số trên với \(m = 3.\)
Với \(m = 3\) ta có hàm số \(y = {x^2} - 4x + 3\)
Trục đối xứng \(x = 2.\)
Đỉnh parabol \(I\left( {2; - 1} \right)\)
Vì \(a > 0\) nên đồ thị hàm số quay bề lõm lên trên
BBT:
Hàm số đồng biến trên \(\left( {2; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ;2} \right)\)
Bảng giá trị:
Đồ thị hàm số:
b) Tìm \(m\) sao cho đồ thị cắt \(Ox\) tại \(2\) điểm phân biệt \(A,\,B\) với \(OA = 3OB.\) (1,5đ)
Xét phương trình hoành độ giao điểm \({x^2} - 4x + m = 0\) (1)
Đồ thị cắt \(Ox\) tại hai điểm phân biệt \( \Leftrightarrow \Delta ' = 4 - m > 0 \Leftrightarrow m < 4\).
Khi đó (1) có hai nghiệm phân biệt \({x_1} = 2 - \sqrt {4 - m} ,{x_2} = 2 + \sqrt {4 - m} \).
TH1: \(A\left( {2 + \sqrt {4 - m} ;0} \right),B\left( {2 - \sqrt {4 - m} ;0} \right)\).
\(OA = 3OB\) \( \Leftrightarrow 2 + \sqrt {4 - m} = 3\left| {2 - \sqrt {4 - m} } \right|\)
\( \Leftrightarrow 4 + 4 - m + 4\sqrt {4 - m} \) \( = 9\left( {4 + 4 - m - 4\sqrt {4 - m} } \right)\)
\( \Leftrightarrow 5\sqrt {4 - m} = 8 - m\) \( \Leftrightarrow \left\{ \begin{array}{l}8 - m \ge 0\\25\left( {4 - m} \right) = 64 - 16m + {m^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m \le 8\\{m^2} + 9m - 36 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m \le 8\\m = 3,m = - 12\end{array} \right.\,\,\,\left( {tm} \right)\)
Vậy \(m = 3, \,\, m=-12\).
TH2: \(A\left( {2 - \sqrt {4 - m} ;0} \right),B\left( {2 + \sqrt {4 - m} ;0} \right)\).
\(OA = 3OB\) \( \Leftrightarrow \left| {2 - \sqrt {4 - m} } \right| = 3\left( {2 + \sqrt {4 - m} } \right)\)
\( \Leftrightarrow 4 + 4 - m - 4\sqrt {4 - m} \) \( = 9\left( {4 + 4 - m + 4\sqrt {4 - m} } \right)\)
\( \Leftrightarrow 5\sqrt {4 - m} = m - 8\) (vô nghiệm do \(m < 4\) thì \(m - 8 < 0\))
Vậy \(m = 3, \,\, m=-12\).
Đáp án cần chọn là: C
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
