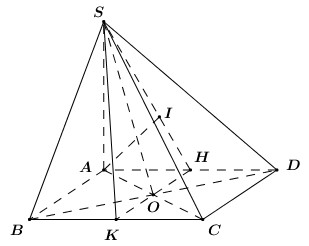
Cho hình chóp \(S.ABCD\) có đáy là hình vuông tâm \(O\) cạnh \(1\). Cạnh bên \(SA\) vuông góc với
Cho hình chóp \(S.ABCD\) có đáy là hình vuông tâm \(O\) cạnh \(1\). Cạnh bên \(SA\) vuông góc với đáy và tam giác \(SBD\) đều. biết khoảng cách giữa \(SO,\,\,CD\) bằng \(\dfrac{{\sqrt a }}{b}\) trong đó \(a,\,\,b\) là các số tự nhiên. Khi đó giá trị của \(a + b\) là:
Đáp án đúng là: B
Quảng cáo
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa đường thẳng này và mặt phẳng chứa đường thẳng kia và song song với đường thẳng này.
- Sử dụng phương pháp đổi đỉnh.
- Áp dụng hệ thức lượng trong tam giác vuông.
Gọi \(H,\,\,K\) lần lượt là trung điểm của \(AD,\,\,BC\) ta có: \(HK\parallel CD\).
\( \Rightarrow d\left( {SO;CD} \right) = d\left( {CD;\left( {SHK} \right)} \right)\) \( = d\left( {C;\left( {SHK} \right)} \right)\).
Ta có: \(AC \cap \left( {SHK} \right) = O\) \( \Rightarrow \dfrac{{d\left( {A;\left( {SHK} \right)} \right)}}{{d\left( {C;\left( {SHK} \right)} \right)}} = \dfrac{{AO}}{{CO}} = 1\)\( \Rightarrow d\left( {C;\left( {SHK} \right)} \right) = d\left( {A;\left( {SHK} \right)} \right)\).
Trong \(\left( {SAD} \right)\) kẻ \(AI \bot SH\,\,\left( {I \in SH} \right)\) ta có:
\(\left\{ \begin{array}{l}HK \bot AH\\HK \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow HK \bot \left( {SAD} \right) \Rightarrow HK \bot AI\).
\(\left\{ \begin{array}{l}AI \bot KH\\AI \bot SH\end{array} \right. \Rightarrow AI \bot \left( {SHK} \right)\)\( \Rightarrow d\left( {A;\left( {SHK} \right)} \right) = AI\)\( \Rightarrow d\left( {SO;CD} \right) = AI\).
Vì \(ABCD\) là hình vuông cạnh \(1\) nên \(AC = BD = \sqrt 2 \).
\( \Rightarrow \) Tam giác \(SBD\) đều cạnh \(\sqrt 2 \) \( \Rightarrow SO = \dfrac{{\sqrt 2 .\sqrt 3 }}{2} = \dfrac{{\sqrt 6 }}{2}.\)
Tam giác SAO vuông tại A có \(SO = \dfrac{{\sqrt 6 }}{2};\,\,AO = \dfrac{{\sqrt 2 }}{2}\).
Áp dụng định lí Pytago ta có: \(SA = \sqrt {S{O^2} - A{O^2}} \) \( = \sqrt {{{\left( {\dfrac{{\sqrt 6 }}{2}} \right)}^2} - {{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^2}} = 1\)
Áp dụng hệ thức lượng trong tam giác vuông \(SAH\) có:
\(\begin{array}{l}AI = \dfrac{{SA.AH}}{{\sqrt {S{A^2} + A{H^2}} }} = \dfrac{{1.\dfrac{1}{2}}}{{\sqrt {1 + \dfrac{1}{4}} }} = \dfrac{{\sqrt 5 }}{5}\\ \Rightarrow a = b = 5 \Rightarrow a + b = 10.\end{array}\)
Đáp án cần chọn là: B
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
