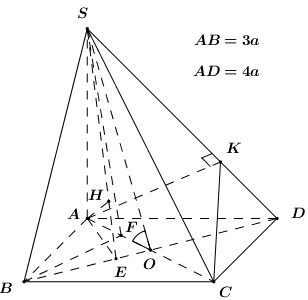
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật có \(AB = 3a,\)\(AD = 4a,\) \(AC \cap BD = O\).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật có \(AB = 3a,\)\(AD = 4a,\) \(AC \cap BD = O\). Biết cạnh \(SA\) vuông góc với đáy và \(SO\) tạo với đáy góc \({60^0}\). Tính góc giữa:
Trả lời cho các câu 1, 2, 3, 4, 5 dưới đây:
\(SC\) và \(\left( {ABCD} \right)\)
Đáp án đúng là: B
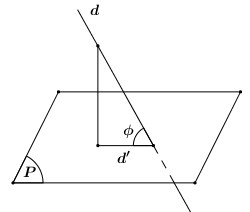
Phương pháp xác định góc giữa đường và mặt.
Bước 1: Tìm giao điểm \(d \cap \left( P \right) = B\) (đỉnh góc)
Bước 2: Từ \(A \in d\), dựng \(AH \bot \left( P \right)\) tại \(H\). Nối \(HB\).
Suy ra \(HB\) là hình chiếu vuông góc của \(AB\) trên \(\left( P \right)\).
Bước 3: Vậy \(\left[ {\widehat {d;\left( P \right)}} \right] = \widehat {\left( {AB;HB} \right)} = \widehat {ABH}\).
Ta có: \(SO \cap \left( {ABCD} \right) = \left\{ O \right\}\) và \(SA \bot \left( {ABCD} \right)\).
Do đó \(AO\) là hình chiếu vuông góc của \(SO\) lên \(\left( {ABCD} \right)\).
\( \Rightarrow \widehat {\left[ {SO;\left( {ABCD} \right)} \right]} = \widehat {\left( {SO;AO} \right)} = \widehat {SOA} = {60^0}\).
Áp dụng định lí Pytago ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{\left( {3a} \right)}^2} + \left( {4{a^2}} \right)} = 5a\).
\( \Rightarrow AO = \dfrac{1}{2}AC = \dfrac{{5a}}{2}\).
Xét \(\Delta SAO\) vuông tại \(A\): \(SA = OA.\tan {60^0} = \dfrac{{5a}}{2}.\sqrt 3 = \dfrac{{5a\sqrt 3 }}{2}\).
\(SC\) và \(\left( {ABCD} \right)\)
Ta có: \(SC \cap \left( {ABCD} \right) = \left\{ C \right\}\) và \(SA \bot \left( {ABCD} \right)\).
Do đó \(AC\) là hình chiếu vuông góc của \(SC\) lên \(\left( {ABCD} \right)\).
\( \Rightarrow \widehat {\left[ {SC;\left( {ABCD} \right)} \right]} = \widehat {\left( {SC;AC} \right)} = \widehat {SCA}\).
Xét \(\Delta SAC\) vuông tại \(A\): \(\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = \dfrac{{\frac{{5a\sqrt 3 }}{2}}}{{5a}} = \dfrac{{\sqrt 3 }}{2}\)
\( \Rightarrow \widehat {SCA} = \arctan \dfrac{{\sqrt 3 }}{2} = {40^0}54'\)
Đáp án cần chọn là: B
\(SD\) và \(\left( {ABCD} \right)\)
Đáp án đúng là: D
Phương pháp xác định góc giữa đường và mặt.
Bước 1: Tìm giao điểm \(d \cap \left( P \right) = B\) (đỉnh góc)
Bước 2: Từ \(A \in d\), dựng \(AH \bot \left( P \right)\) tại \(H\). Nối \(HB\).
Suy ra \(HB\) là hình chiếu vuông góc của \(AB\) trên \(\left( P \right)\).
Bước 3: Vậy \(\left[ {\widehat {d;\left( P \right)}} \right] = \widehat {\left( {AB;HB} \right)} = \widehat {ABH}\).
\(SD\) và \(\left( {ABCD} \right)\)
Ta có: \(SD \cap \left( {ABCD} \right) = \left\{ D \right\}\) và \(SA \bot \left( {ABCD} \right)\).
Do đó \(AD\) là hình chiếu vuông góc của \(SD\) lên \(\left( {ABCD} \right)\).
\( \Rightarrow \widehat {\left[ {SD;\left( {ABCD} \right)} \right]} = \widehat {\left( {SD;AD} \right)} = \widehat {SDA}\).
Xét \(\Delta SAD\) vuông tại \(A\): \(\tan \widehat {SDA} = \dfrac{{SA}}{{AD}} = \dfrac{{\dfrac{{5a\sqrt 3 }}{2}}}{{4a}} = \dfrac{{5\sqrt 3 }}{8}\).
\( \Rightarrow \widehat {SDA} = \arctan \dfrac{{5\sqrt 3 }}{8} = {47^0}16'\).
Đáp án cần chọn là: D
\(SA\) và \(\left( {SBD} \right)\)
Đáp án đúng là: A
Phương pháp xác định góc giữa đường và mặt.
Bước 1: Tìm giao điểm \(d \cap \left( P \right) = B\) (đỉnh góc)
Bước 2: Từ \(A \in d\), dựng \(AH \bot \left( P \right)\) tại \(H\). Nối \(HB\).
Suy ra \(HB\) là hình chiếu vuông góc của \(AB\) trên \(\left( P \right)\).
Bước 3: Vậy \(\left[ {\widehat {d;\left( P \right)}} \right] = \widehat {\left( {AB;HB} \right)} = \widehat {ABH}\).
\(SA\) và \(\left( {SBD} \right)\)
Kẻ \(AE \bot BD,\,\,AH \bot SE\).
Vì \(BD \bot AE,\,\,BD \bot SA\) \( \Rightarrow BD \bot \left( {SAE} \right) \Rightarrow BD \bot AH\).
Vì \(AH \bot SE,\,\,AH \bot BD\) \( \Rightarrow AH \bot \left( {SBD} \right)\).
Ta có: \(SA \cap \left( {SBD} \right) = \left\{ S \right\}\) và \(AH \bot \left( {SBD} \right)\).
Do đó \(SH\) là hình chiếu vuông góc của \(SA\) lên \(\left( {SBD} \right)\).
\( \Rightarrow \widehat {\left[ {SA;\left( {SBD} \right)} \right]} = \widehat {\left( {SA;SH} \right)} = \widehat {ASH} = \widehat {ASE}\).
Áp dụng hệ thức lượng trong tam giác vuông \(ABD\) ta có:
\(\dfrac{1}{{A{E^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{D^2}}}\) \( = \dfrac{1}{{{{\left( {3a} \right)}^2}}} + \dfrac{1}{{{{\left( {4a} \right)}^2}}} = \dfrac{{25}}{{144{a^2}}}\) \( \Rightarrow AE = \dfrac{{12a}}{5}\).
Xét \(\Delta SAE\) vuông tại \(A\): \(\tan \widehat {ASE} = \dfrac{{AE}}{{SA}} = \dfrac{{\dfrac{{12a}}{5}}}{{\dfrac{{5a\sqrt 3 }}{2}}} = \dfrac{{8\sqrt 3 }}{{25}}\).
\( \Rightarrow \widehat {ASE} = \arctan \dfrac{{8\sqrt 3 }}{{25}} = {29^0}\).
Đáp án cần chọn là: A
\(SB\) và \(\left( {SAC} \right)\)
Đáp án đúng là: A
Phương pháp xác định góc giữa đường và mặt.
Bước 1: Tìm giao điểm \(d \cap \left( P \right) = B\) (đỉnh góc)
Bước 2: Từ \(A \in d\), dựng \(AH \bot \left( P \right)\) tại \(H\). Nối \(HB\).
Suy ra \(HB\) là hình chiếu vuông góc của \(AB\) trên \(\left( P \right)\).
Bước 3: Vậy \(\left[ {\widehat {d;\left( P \right)}} \right] = \widehat {\left( {AB;HB} \right)} = \widehat {ABH}\).
\(SB\) và \(\left( {SAC} \right)\)
Kẻ \(BF \bot AC\).
Vì \(BF \bot AC,\,\,BF \bot SA\) \( \Rightarrow BF \bot \left( {SAC} \right)\).
Ta có: \(SB \cap \left( {SAC} \right) = \left\{ S \right\}\) và \(BF \bot \left( {SAC} \right)\).
Do đó \(SF\) là hình chiếu vuông góc của \(SB\) lên \(\left( {SAC} \right)\).
\( \Rightarrow \widehat {\left[ {SB;\left( {SAC} \right)} \right]} = \widehat {\left( {SB;SF} \right)} = \widehat {BSF}\).
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) ta có:
\(\dfrac{1}{{B{F^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{B{C^2}}}\) \( = \dfrac{1}{{{{\left( {3a} \right)}^2}}} + \dfrac{1}{{{{\left( {4a} \right)}^2}}} = \dfrac{{25}}{{144{a^2}}}\) \( \Rightarrow BF = \dfrac{{12a}}{5}\).
Áp dụng định lí Pytago trong tam giác vuông \(SAB\) có:
\(SB = \sqrt {S{A^2} + A{B^2}} = \sqrt {{{\left( {\dfrac{{5a\sqrt 3 }}{2}} \right)}^2} + {{\left( {3a} \right)}^2}} = \dfrac{{a\sqrt {111} }}{2}\).
Xét \(\Delta SBF\) vuông tại \(F\): \(\sin \widehat {BSF} = \dfrac{{BF}}{{SB}} = \dfrac{{\dfrac{{12a}}{5}}}{{\dfrac{{a\sqrt {111} }}{2}}} = \dfrac{{24}}{{5\sqrt {111} }}\).
\( \Rightarrow \widehat {BSF} = \arcsin \dfrac{{24}}{{5\sqrt {111} }} = {27^0}6'\).
Đáp án cần chọn là: A
\(AC\) và \(\left( {SCD} \right)\)
Đáp án đúng là: C
Phương pháp xác định góc giữa đường và mặt.
Bước 1: Tìm giao điểm \(d \cap \left( P \right) = B\) (đỉnh góc)
Bước 2: Từ \(A \in d\), dựng \(AH \bot \left( P \right)\) tại \(H\). Nối \(HB\).
Suy ra \(HB\) là hình chiếu vuông góc của \(AB\) trên \(\left( P \right)\).
Bước 3: Vậy \(\left[ {\widehat {d;\left( P \right)}} \right] = \widehat {\left( {AB;HB} \right)} = \widehat {ABH}\).
\(AC\) và \(\left( {SCD} \right)\)
Kẻ \(AK \bot SD\).
Vì \(CD \bot AD,\,\,CD \bot SA\) \( \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot AK\).
Vì \(AK \bot SD,\,\,AK \bot CD\) \( \Rightarrow AK \bot \left( {SCD} \right)\).
Ta có: \(AC \cap \left( {SCD} \right) = \left\{ C \right\}\) và \(AK \bot \left( {SCD} \right)\).
Do đó \(KC\) là hình chiếu vuông góc của \(AC\) lên \(\left( {SCD} \right)\).
\( \Rightarrow \widehat {\left[ {AC;\left( {SCD} \right)} \right]} = \widehat {\left( {AC;KC} \right)} = \widehat {ACK}\).
Áp dụng hệ thức lượng trong tam giác vuông \(SAD\) ta có:
\(\dfrac{1}{{A{K^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{D^2}}}\) \( = \dfrac{1}{{{{\left( {\dfrac{{5a\sqrt 3 }}{2}} \right)}^2}}} + \dfrac{1}{{{{\left( {4a} \right)}^2}}} = \dfrac{{139}}{{1200{a^2}}}\) \( \Rightarrow AK = a\sqrt {\dfrac{{1200}}{{139}}} \).
Xét \(\Delta ACK\) vuông tại \(K\): \(\sin \widehat {ACK} = \dfrac{{AK}}{{AC}} = \dfrac{{a\sqrt {\dfrac{{1200}}{{139}}} }}{{5a}} = \dfrac{{\sqrt {\dfrac{{1200}}{{139}}} }}{5}\).
\( \Rightarrow \widehat {ACK} = \arcsin \dfrac{{\sqrt {\dfrac{{1200}}{{139}}} }}{5} = {35^0}59'\).
Đáp án cần chọn là: C
Quảng cáo
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
