Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước
Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo.
● Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1 g hương liệu;
● Để pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu.
Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
Đáp án đúng là: C
Quảng cáo
- Gọi \(x,{\rm{ }}y\) lần lượt là số lít nước cam và số lít nước táo mà mỗi đội cần pha chế.
- Biểu diễn số gam đường, số lít ngước, số gam hương liệu cần dùng theo \(x,{\rm{ }}y\).
- Sử dụng dữ kiện bài cho để lập hệ bất phương trình ẩn \(x,{\rm{ }}y\).
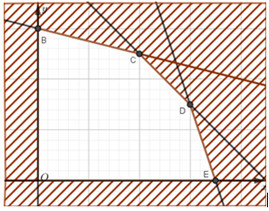
- Xác định miền nghiệm của bất phương trình trên mặt phẳng tọa độ.
- Xác định hàm số điểm thưởng nhận được \(F\left( {x;y} \right)\) và tìm \(\max F\left( {x;y} \right)\).
Giả sử \(x,{\rm{ }}y\) lần lượt là số lít nước cam và số lít nước táo mà mỗi đội cần pha chế.
Suy ra \(30x + 10y\) là số gam đường cần dùng;
\(x + y\) là số lít nước cần dùng;
\(x + 4y\) là số gam hương liệu cần dùng.
Theo giả thiết ta có \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\30x + 10y \le 210\\x + y \le 9\\x + 4y \le 24\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\y \ge 0\\3x + y \le 21\\x + y \le 9\\x + 4y \le 24\end{array} \right..\) \(\left( * \right)\)
Số điểm thưởng nhận được sẽ là \(P\left( {x;y} \right) = 60x + 80y.\)
Ta đi tìm giá trị nhỏ nhất của biểu thức \(P\) với \(x,{\rm{ }}y\) thỏa mãn \(\left( * \right)\).
Miền nghiệm là phần hình vẽ không tô màu ở hình trên, hay là ngũ giác \(OBCDE\) với \(O\left( {0;0} \right),\) \(B\left( {0;6} \right),\) \(C\left( {4;5} \right),\) \(D\left( {6;3} \right),\) \(E\left( {7;0} \right)\).
Biểu thức \(P = 60x + 80y\) đạt GTLN tại \(\left( {x;y} \right)\) là tọa độ một trong các đỉnh của ngũ giác.
Thay lần lượt tọa độ các điểm \(O,B,C,D,E\) vào biểu thức \(P\left( {x;y} \right)\) ta được:
\(\begin{array}{l}P\left( {0;0} \right) = 0\\P\left( {0;6} \right) = 480\\P\left( {4;5} \right) = 640\\P\left( {6;3} \right) = 600\\P\left( {7;0} \right) = 420\end{array}\)
Đáp án cần chọn là: C
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
