Bất Đẳng thức, Giá trị lớn nhất và nhỏ nhất
Cho các số thực dương a, b, c thỏa mãn điều kiện a + b + c = 3. Chứng minh rằng: 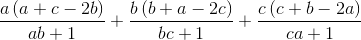 ≥ 0
≥ 0
Đáp án đúng là: A
Quảng cáo
Đáp án cần chọn là: A
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn

-
024.7300.7989
-
1800.6947

(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com



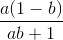 + 1 +
+ 1 + 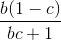 + 1 +
+ 1 + 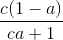 + 1 ≥ 3
+ 1 ≥ 3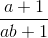 +
+ 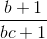 +
+ 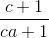 ≥ 3 (*)
≥ 3 (*)![3\sqrt[3]e_\frace_\left( {a + 1} \right)\left( {b + 1} \right)\left( {c + 1} \right)e_\left( {ab + 1} \right)\left( {bc + 1} \right)\left( {ca + 1} \right)](http://images.tuyensinh247.com/picture/learning/exam/2014/0402/v37504_895617_3.gif)
![\sqrt[3]{abc}](http://images.tuyensinh247.com/picture/learning/exam/2014/0423/v37504_513710_8.gif) =>
=> 







