Đặt điện áp \(u = U\sqrt 2 .\cos \omega t\) (U không đổi, ɷ thay đổi được) vào hai đầu đoạn

Câu hỏi số 410669:

Vận dụng cao

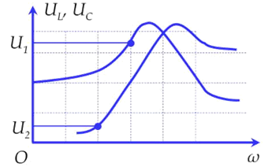
Đặt điện áp \(u = U\sqrt 2 .\cos \omega t\) (U không đổi, ɷ thay đổi được) vào hai đầu đoạn mạch gồm điện trở, cuộn cảm thuần và tụ điện mắc nối tiếp. Hình vẽ bên là một phần đồ thị biểu diễn sự phụ thuộc của điện áp hiệu dụng hai đầu cuộn cảm và hai đầu tụ điện theo ɷ. Tỷ số \(\frac{{{U_1}}}{{{U_2}}}\) là:

A. 5,49

B. 5,21

C. 4,80

D. 5,0

Đáp án đúng là: A

Quảng cáo

Xem lời giải

Câu hỏi:410669

Phương pháp giải

Sử dụng phương pháp chuẩn hóa.

Từ đồ thị ta thấy đường đạt cực đại trước là U_C ; đường đạt cực đại sau là U_L.

Vị trí U_L cắt U_Clà vị trí xảy ra cộng hưởng ứng với \({\omega _0} = \frac{1}{{\sqrt {LC} }}\) ứng với 4 đơn vị chia trên trục U, tức là \({U_L} = {U_C} = 4\).

Từ đồ thị ta thấy vị trí U₁ (U_C1) ứng với \({\omega _1} = \frac{3}{4}{\omega _0}\)

Vị trí U₂ (U_L2) ứng với \({\omega _2} = \frac{1}{2}{\omega _0}\)

Tại vị trí ban đầu của U_C khi ω = 0 thì U_C = U bằng 2 đơn vị chia trên trục U.

Tỉ số

\(\frac{{{U_1}}}{{{U_2}}} = \frac{{{U_{C1}}}}{{{U_{L2}}}} = \frac{U}{{{Z_1}}}.{Z_{C1}}.\frac{{{Z_2}}}{U}.{Z_{L2}} = \frac{{\frac{1}{{{\omega _1}C}}}}{{\sqrt {{R^2} + {{\left( {{\omega _1}L - \frac{1}{{{\omega _1}C}}} \right)}^2}} }}.\sqrt {{R^2} + {{\left( {{\omega _2}L - \frac{1}{{{\omega _2}C}}} \right)}^2}} .{\omega _2}.L\)

Giải chi tiết

Sử dụng phương pháp chuẩn hóa.

Từ đồ thị ta thấy đường đạt cực đại trước là U_C ; đường đạt cực đại sau là U_L.

Tại vị trí ban đầu của U_C khi ɷ = 0 thì:

\(\begin{array}{l}
{U_C} = \frac{U}{{\sqrt {{R^2} + {{\left( {\omega L - \frac{1}{{\omega C}}} \right)}^2}} }}.\frac{1}{{\omega C}} = \frac{U}{{C.\sqrt {{\omega ^2}.{R^2} + {\omega ^4}L - {\omega ^2}.\frac{L}{C} + \frac{1}{{{C^2}}}} }}\\
\Rightarrow \omega = 0 \Rightarrow {U_C} = U
\end{array}\)

bằng 2 đơn vị chia trên trục điện áp. Chuẩn hóa U = 2.

Vị trí U_L cắt U_C là vị trí xảy ra cộng hưởng ứng với \({\omega _0} = \frac{1}{{\sqrt {LC} }}\) ứng với 4 đơn vị chia trên trục U, tức là:

\(\left\{ \begin{array}{l}
{U_L} = {U_C} = {\rm{ }}4{\rm{ }}\\
{U_R} = U = 2
\end{array} \right. \Rightarrow {Z_{L0}} = {Z_{C0}} = 2R\)

Chuẩn hóa số liệu, đặt

\(R = 1 \Rightarrow {Z_{L0}} = {Z_{C0}} = 2\)

Từ đồ thị ta thấy vị trí U₁ (U_C1) ứng với

\({\omega _1} = \frac{3}{4}{\omega _0}\)

Vị trí U₂ (U_L2) ứng với \({\omega _2} = \frac{1}{2}{\omega _0}\)

Ta có tỉ số:

\(\begin{array}{l}
\frac{{{U_1}}}{{{U_2}}} = \frac{{{U_{C1}}}}{{{U_{L2}}}} = \frac{U}{{{Z_1}}}.{Z_{C1}}.\frac{{{Z_2}}}{{U.{Z_{L2}}}}\\
\Rightarrow \frac{{{U_1}}}{{{U_2}}} = \frac{{\frac{1}{{{\omega _1}C}}}}{{\sqrt {{R^2} + {{\left( {{\omega _1}L - \frac{1}{{{\omega _1}C}}} \right)}^2}} }}.\sqrt {{R^2} + {{\left( {{\omega _2}L - \frac{1}{{{\omega _2}C}}} \right)}^2}} .\frac{1}{{{\omega _2}.L}}
\end{array}\)

Theo chuẩn hóa ta được:

\(\frac{{\frac{4}{3}.2}}{{\sqrt {1 + {{\left( {\frac{3}{4}.2 - \frac{4}{3}.2} \right)}^2}} }}.\frac{{\sqrt {1 + {{\left( {0,5.2 - \frac{2}{{0,5}}} \right)}^2}} }}{{0,5.2}} = 5,487\)

Vậy tỉ số gần nhất với giá trị 5,49

Đáp án cần chọn là: A

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.