Tìm tập hợp các giá trị thực của tham số \(m\) để phương trình \(m{\sin ^2}x - 3\sin x\cos x - m -
Tìm tập hợp các giá trị thực của tham số \(m\) để phương trình \(m{\sin ^2}x - 3\sin x\cos x - m - 1 = 0\) có đúng ba nghiệm thuộc khoảng \(\left( {0;\dfrac{{3\pi }}{2}} \right)\).
Đáp án đúng là: B
Quảng cáo
- Xét 2 TH: \(\cos x = 0\) và \(\cos x \ne 0\). Chứng minh trường hợp \(\cos x = 0\) không thỏa mãn, khi \(\cos x \ne 0\), chia cả 2 vế của phương trình cho \({\cos ^2}x\).
- Đặt ẩn phụ \(t = \tan x\), đưa phương trình về dạng phương trình bậc hai ẩn \(t\).
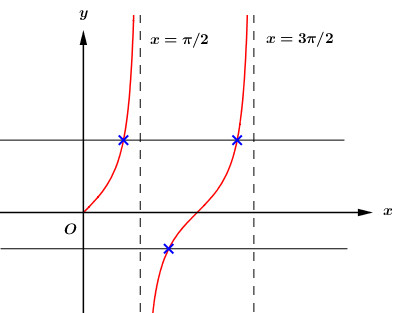
- Xét đồ thị hàm số \(t = \tan x\) trên \(\left( {0;\dfrac{{3\pi }}{2}} \right)\), xác định trên từng khoảng cụ thể mỗi giá trị \(t\) cho bao nhiêu giá trị \(x\) tương ứng, từ đó suy ra điều kiện của nghiệm của phương trình bậc hai ẩn \(t\).
- Phương trình dạng \(a{x^2} + bx + c = 0\,\,\left( {a \ne 0} \right)\) có 2 nghiệm trái dấu \( \Leftrightarrow ac < 0\).
TH1: \(\cos x = 0\), khi đó phương trình trở thành: \( - m - 1 = 0 \Leftrightarrow m = - 1\).
Với \(\cos x = 0 \Leftrightarrow x = \dfrac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Cho \(x \in \left( {0;\dfrac{{3\pi }}{2}} \right)\) \( \Rightarrow 0 < \dfrac{\pi }{2} + k\pi < \dfrac{{3\pi }}{2} \Leftrightarrow - \dfrac{1}{2} < k < 1,\,\,k \in \mathbb{Z}\) \( \Rightarrow k = 0\).
Khi đó phương trình đã cho chỉ có 1 nghiệm thuộc \(\left( {0;\dfrac{{3\pi }}{2}} \right)\), do đó TH \(\cos x = 0\) không thỏa mãn.
TH2: \(\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Chia cả 2 vế của phương trình ban đầu cho \({\cos ^2}x\) ta được:
\(\begin{array}{l}m{\tan ^2}x - 3\tan x + \left( { - m - 1} \right)\left( {1 + {{\tan }^2}x} \right) = 0\\ \Leftrightarrow m{\tan ^2}x - 3\tan x - m - m{\tan ^2}x - 1 - {\tan ^2}x = 0\\ \Leftrightarrow - {\tan ^2}x - 3\tan x - m - 1 = 0\\ \Leftrightarrow {\tan ^2}x + 3\tan x + m + 1 = 0\,\,\,\left( * \right)\end{array}\)
Đặt \(t = \tan x\), phương trình (*) trở thành: \({t^2} + 3t + m + 1 = 0\,\,\left( {**} \right)\).
Xét đồ thị hàm số \(t = \tan x\) trên \(\left( {0;\dfrac{{3\pi }}{2}} \right)\) ta thấy:
+ Với mỗi giá trị \(t > 0\) thì một giá trị của \(t\) cho ta 2 giá trị của \(x\) tương ứng.
+ Với mỗi giá trị \(t < 0\) thì một giá trị của \(t\) cho ta 1 giá trị của \(x\) tương ứng.
Do đó để phương trình ban đầu có 3 nghiệm phân biệt thuộc \(\left( {0;\dfrac{{3\pi }}{2}} \right)\) thì phương trình (**) phải có 2 nghiệm \(t\) trái dấu \( \Leftrightarrow ac < 0 \Leftrightarrow m + 1 < 0 \Leftrightarrow m < - 1\).
Vậy \(m \in \left( { - \infty ; - 1} \right)\).
Đáp án cần chọn là: B
Group 2K9 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
