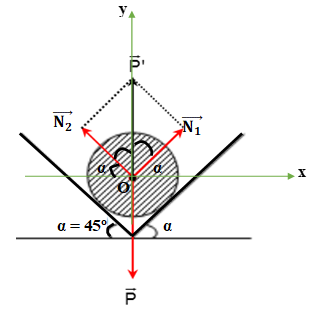
Hai mặt phẳng đỡ tạo với mặt phẳng nằm ngang các góc \(\alpha = {45^0}\). Trên hai mặt phẳng
Hai mặt phẳng đỡ tạo với mặt phẳng nằm ngang các góc \(\alpha = {45^0}\). Trên hai mặt phẳng đó người ta đặt một quả cầu đồng chất có khối lượng 2kg (Hình vẽ). Bỏ qua ma sát và lấy \(g = 10{\rm{ }}m/{s^2}\). Hỏi áp lực của quả cầu lên mỗi mặt phẳng đỡ bằng bao nhiêu?
Đáp án đúng là: C
Quảng cáo
Điều kiện cân bằng của một chất điểm là hợp lực của các lực tác dụng lên nó phải bằng 0:
\(\vec F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... = \vec 0\)
Lực tác dụng lên quả cầu được biểu diễn như hình vẽ:
Khi hệ cân bằng ta có: \(\vec P + \overrightarrow {{N_1}} + \overrightarrow {{N_2}} = \vec 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)\)
Chọn hệ trục toạ độ Oxy như hình vẽ.
Chiếu phương trình (1) lên các trục Ox, Oy ta có :
\(\begin{array}{*{20}{l}}\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{{N_1}.\cos \alpha - {N_2}.\cos \alpha = 0}\\{ - P + {N_1}.\sin \alpha + {N_2}.\sin \alpha = 0}\end{array}} \right.\\ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{N_1} = {N_2}}\\{P = {N_1}.\sin \alpha + {N_2}.\sin \alpha }\end{array}} \right. \Rightarrow P = 2{N_1}\sin \alpha \end{array}\\\begin{array}{l} \Rightarrow {N_1} = \dfrac{P}{{2\sin \alpha }} = \dfrac{{mg}}{{2\sin \alpha }} = \dfrac{{2.10}}{{2.\sin 45}} \approx 14N\\ \Rightarrow {N_1} = {N_2} = 14N\end{array}\end{array}\)
Đáp án cần chọn là: C
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
