Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại I cần 2kg nguyên liệu và 30
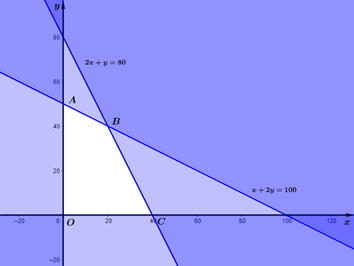
Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại I cần 2kg nguyên liệu và 30 giờ, đem lại mức lời \(40000\) đồng. Mỗi kg sản phẩm loại II cần \(4kg\) nguyên liệu và \(15\) giờ, đem lại mức lời \(30000\) đồng. Xưởng có \(200kg\) nguyên liệu và \(1200\) giờ làm việc. Hỏi sản xuất mỗi loại sản phẩm lần lượt là bao nhiêu để có mức lời cao nhất?
Đáp án đúng là: A
Quảng cáo
Bước 1: Chuyển các điều kiện trong bài toán kinh tế thành 1 hệ bất phương trình bậc nhất hai ẩn
Bước 2: Vẽ và xác định miền nghiệm \(S\) của hệ bất phương trình trên mặt phẳng tọa độ \(Oxy\).
Bước 3: Biểu diễn hàm cần tối ưu \(F\left( {x;\,\,y} \right) = ax + by\) theo các ẩn \(x;\,\,y \in S\)
Bước 4: Thay tọa độ các đỉnh của miền nghiệm vào \(F\left( {x;\,\,y} \right)\) để tìm \({F_{\min }}\) hoặc \({F_{\max }}\) để kết luận.
Gọi \(x,\,\,y\) là số \(kg\) loại \(I,\,\,II\) cần sản xuất \(\left( {x,\,\,y \ge 0} \right)\).
Số tiền lãi là \(40000x + 30000y\) (đồng)
Theo đề bài, ta có hệ bất phương trình \(\left\{ \begin{array}{l}x + 2y - 100 \le 0\\2x + y - 80 \le 0\\x \ge 0\\y \ge 0\end{array} \right.\,\,\left( I \right)\)
Yêu cầu bài toán trở thành: Tìm \(x,\,\,y\) thỏa mãn hệ bất phương trình \(\left( I \right)\) sao cho \(F\left( {x,\,\,y} \right) = 40000x + 30000y\) lớn nhất.
Vẽ và xác định miền nghiệm của \(\left( I \right)\):
+) Miền nghiệm của \(\left( I \right)\) là tứ giác \(OABC\) (kể cả biên)
+) \(A\left( {0;\,\,50} \right),\,\,B\left( {20;\,\,40} \right),\,\,C\left( {40;\,\,0} \right),\,\,O\left( {0;\,\,0} \right)\)
+) \(F\left( {x,\,\,y} \right) = 40000x + 30000y\)
\(F\left( A \right) = 1500000;\,\,F\left( B \right) = 2000000;\,\,F\left( C \right) = 1600000;\,\,F\left( O \right) = 0\)
\( \Rightarrow \max F\left( {x;\,\,y} \right) = F\left( B \right) = 2000000 \Leftrightarrow x = 20;\,\,y = 40\)
Vậy cần sản xuất loại \(I\) là \(20kg\), loại \(II\) là \(40kg\) để có mức lời cao nhất.
Đáp án cần chọn là: A
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
 |
 |
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
