Cho cơ hệ như hình vẽ, lò xo và đĩa có khối lượng không đáng kể, lò xo có độ cứng \(k =

Câu hỏi số 531019:

Vận dụng cao

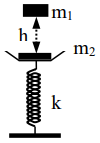
Cho cơ hệ như hình vẽ, lò xo và đĩa có khối lượng không đáng kể, lò xo có độ cứng \(k = 50N/m\), vật \({m_1} = 200g\) vật \({m_2} = 300g\). Khi \({m_2}\) đang cân bằng ta thả \({m_1}\) rơi tự do từ độ cao h (so với \({m_2}\)). Sau va chạm \({m_1}\) dính chặt với \({m_2}\), cả hai cùng dao động với biên độ \(A = 7cm\), lấy \(g = 10m/{s^2}\). Độ cao h là

A. 6,25cm.

B. 10,31cm.

C. 26,25cm

D. 32,81cm

Đáp án đúng là: B

Quảng cáo

Xem lời giải

Câu hỏi:531019

Phương pháp giải

Tần số góc: \(\omega = \sqrt {\dfrac{k}{m}} \)

Vật nặng cân bằng khi: \({F_{dh}} = P \Leftrightarrow k.\Delta l = mg\)

Công thức liên hệ giữa s,v,a của chuyển động thẳng biến đổi đều: \({v^2} - v_0^2 = 2a.s\)

Áp dụng định luật bảo toàn động lượng tính được vận tốc của hệ ngay sau va chạm.

Biên độ dao động: \(A = \sqrt {{x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}} \)

Giải chi tiết

+ Vận tốc của vật \({m_1}\) khi chạm vào \({m_2}\) là: \(v = \sqrt {2gh} \)

+ Vận tốc \({v_0}\) của hệ hai vật ngay sau va chạm là:

\(\left( {{m_1} + {m_2}} \right).{v_0} = {m_1}v \Rightarrow {v_0} = \dfrac{{{m_1}}}{{{m_1} + {m_2}}}.\sqrt {2gh} \)

\( \Rightarrow {v_0} = \dfrac{{0,2}}{{0,2 + 0,3}}.\sqrt {2.10.h} = 0,8\sqrt {5h} \)

+ Khi đo vị trí của hệ hai vật cách vị trí cân bằng của hệ đoạn:

\({x_0} = \Delta l - \Delta {l_0} = \dfrac{{\left( {{m_1} + {m_2}} \right).g}}{k} - \dfrac{{{m_2}g}}{k}\)

\( \Rightarrow {x_0} = \dfrac{{{m_1}g}}{k} = \dfrac{{0,2.10}}{{50}} = 0,04m\)

+ Tần số dao động của hệ:

\(\omega = \sqrt {\dfrac{k}{{{m_1} + {m_2}}}} = \sqrt {\dfrac{{50}}{{0,2 + 0,3}}} = 10rad/s\)

+ Biên độ dao động của hệ:

\({A^2} = x_0^2 + \dfrac{{v_0^2}}{{{\omega ^2}}} \Leftrightarrow 0,{07^2} = \sqrt {0,{{04}^2} + \dfrac{{{{\left( {0,8\sqrt {5h} } \right)}^2}}}{{{{10}^2}}}} \)

\( \Rightarrow h = 0,1031m = 10,31cm\)

Đáp án cần chọn là: B

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Câu hỏi trước Câu tiếp theo

>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.