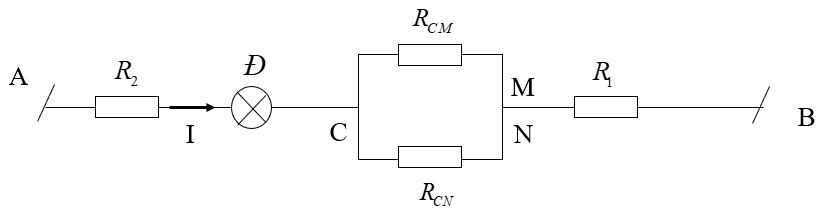
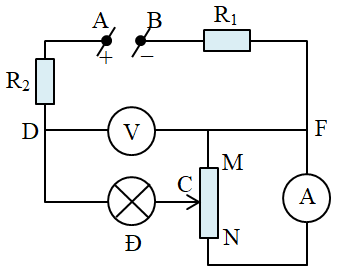
Cho mạch điện như hình vẽ bên. Trong đó: \({U_{AB}} = 6V\); \({R_1} = 1,25\Omega \); \({R_2} = 0,75\Omega
Cho mạch điện như hình vẽ bên. Trong đó: \({U_{AB}} = 6V\); \({R_1} = 1,25\Omega \); \({R_2} = 0,75\Omega \); Đ là bóng đèn loại 1V – 1W, MN là biến trở có điện trở toàn phần \({R_{MN}} = 20\Omega \), biết điện trở tỉ lệ với độ dài. Điện trở của vôn kế vô cùng lớn, điện trở của ampe kế rất nhỏ, điện trở của bóng đèn Đ xem như không thay đổi, bỏ qua điện trở của dây nối.
a) Điều chỉnh con chạy C của biến trở ở đúng vị trí chính giữa của đoạn MN. Xác định số chỉ của ampe kế và vôn kế lúc đó. Nhận xét độ sáng của đèn lúc này.
b) Phải điều chỉnh con chạy C của biến trở đến vị trí nào trên biến trở để công suất tiêu thụ trên toàn bộ biến trở đạt giá trị cực đại? Tính giá trị cực đại đó. So sánh độ sáng của đèn lúc này so với trường hợp ở câu a.
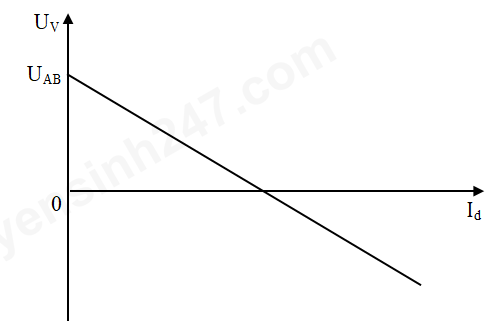
c) Vẽ đồ thị sự phụ thuộc của điện áp hai đầu vôn kế \(\left( {{U_V}} \right)\) theo cường độ dòng điện chạy qua đèn Đ \(\left( {{I_d}} \right)\) khi con chạy C dịch chuyển xuống phía N từ vị trí ở câu a.
Quảng cáo
Cường độ dòng điện: \(I = \dfrac{U}{R}\)
Điện trở bóng đèn: \({R_d} = \dfrac{{{U_{dm}}^2}}{{{P_{dm}}}}\)
Đèn sáng bình thường khi: \(\left\{ \begin{array}{l}{U_d} = {U_{dm}}\\{I_d} = {I_{dm}}\end{array} \right.\)
Bất đẳng thức Cauchy: \(a + b \ge 2\sqrt {ab} \) (dấu “=” xảy ra \( \Leftrightarrow a = b\))
a) Sơ đồ mạch điện: \({R_2}ntDnt\left( {{R_{CM}}//{R_{CN}}} \right)nt{R_1}\)
Điện trở của đèn là: \({R_d} = \dfrac{{U_{dm}^2}}{{{P_{dm}}}} = \dfrac{{{1^2}}}{1} = 1\,\,\left( \Omega \right)\)
Khi \({R_{CM}} = {R_{CN}} = 10\,\,\left( \Omega \right)\), điện trở tương đương cả mạch là:
\({R_{td}} = {R_2} + {R_d} + \dfrac{{{R_{CM}}.{R_{CN}}}}{{{R_{CM}} + {R_{CN}}}} + {R_1} = 8\,\,\left( \Omega \right)\)
Cường độ dòng điện mạch chính là:
\(I = \dfrac{{{U_{AB}}}}{{{R_{td}}}} = \dfrac{6}{8} = 0,75\,\,\left( A \right)\)
Công suất đèn là: \({P_d} = {I^2}{R_d} = 0,56 < {P_{dm}} \to \) đèn sáng yếu.
Ampe kế chỉ cường độ dòng điện qua \({R_{CN}}\), do \({R_{CN}} = {R_{CM}}\) nên \({I_a} = \dfrac{I}{2} = 0,375\,\left( A \right)\)
Số chỉ Vôn kế:
\({U_{DF}} = {U_d} + {U_{CM}} = I{R_d} + \dfrac{I}{2}.{R_{CM}} = 4,5\,\,\left( V \right)\)
b) Đặt \(R = \dfrac{{{R_{CM}}.{R_{CN}}}}{{{R_{CM}} + {R_{CN}}}}\), điện trở tương đương cả mạch:
\({R_{td}} = {R_2} + {R_d} + R + {R_1} = R + 3\,\,\left( \Omega \right)\)
Cường độ dòng điện mạch chính: \(I = \dfrac{U}{{{R_{td}}}} = \dfrac{6}{{R + 3}}\)
Công suất tiêu thụ trên toàn bộ biến trở:
\({P_R} = {I^2}R = \dfrac{{{6^2}.R}}{{{{\left( {R + 3} \right)}^2}}} = \dfrac{{36}}{{R + \dfrac{9}{R} + 6}}\)
Áp dụng bất đẳng thức Cauchy, ta có:
\(R + \dfrac{9}{R} \ge 2\sqrt {R.\dfrac{9}{R}} = 6\) nên \({P_R} \le \dfrac{{36}}{{6 + 6}} = 3\,\,\left( W \right)\)
Dấu “=” xảy ra khi và chỉ khi: \(R = \dfrac{9}{R} \Rightarrow R = 3\,\,\left( \Omega \right)\)
Khi đó, \(\dfrac{{{R_{CM}}.{R_{CN}}}}{{{R_{CM}} + {R_{CN}}}} = 3 \Rightarrow \dfrac{{{R_{CM}}\left( {20 - {R_{CM}}} \right)}}{{20}} = 3\)
\( \Rightarrow - R_{CM}^2 + 20{R_{CM}} - 60 = 0 \Rightarrow \left[ \begin{array}{l}{R_{CM}} = 16,32\,\,\left( \Omega \right)\\{R_{CM}} = 3,68\,\,\left( \Omega \right)\end{array} \right.\)
Công suất đèn: \({P_d} = {I^2}{R_d} = \dfrac{{{6^2}.1}}{{{{\left( {3 + 3} \right)}^2}}} = 1\,\,\left( W \right) = {P_{dm}} \to \) đèn sáng bình thường.
c) Gọi Rb là điện trở biến trở, ta có:
\({U_V} = {I_d}{R_d} + {I_d}{R_b} = {U_{AB}} - {I_d}\left( {{R_1} + {R_2}} \right)\)
→ đồ thị \({U_V}\) theo \({I_d}\) là đường thẳng.
PH/HS 2K10 THAM GIA NHÓM ĐỂ CẬP NHẬT ĐIỂM THI, ĐIỂM CHUẨN MIỄN PHÍ!
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
Hỗ trợ - Hướng dẫn
-
024.7300.7989
-
1800.6947
(Thời gian hỗ trợ từ 7h đến 22h)
Email: lienhe@tuyensinh247.com
